题目内容
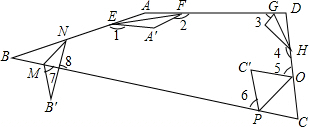 如图,四边形ABCD纸片中,已知∠A=160°,∠B=30°,∠C=60°,四边形ABCD纸片分别沿EF,GH,OP,MN折叠,使A与A′、B与B′、C与C′、D与D′重合,则∠1+∠2+∠3+∠4+∠5+∠6+∠7-∠8的值是( )
如图,四边形ABCD纸片中,已知∠A=160°,∠B=30°,∠C=60°,四边形ABCD纸片分别沿EF,GH,OP,MN折叠,使A与A′、B与B′、C与C′、D与D′重合,则∠1+∠2+∠3+∠4+∠5+∠6+∠7-∠8的值是( )| A、600° | B、700° |
| C、720° | D、800° |
考点:多边形内角与外角
专题:
分析:先根据四边形内角和等于360°得出∠D的度数,根据三角形内角和定理和折叠的性质可以分别得到∠1+∠2,∠3+∠4,∠5+∠6的度数,根据三角形外角的性质和折叠的性质可以得到∠7-∠8的度数,再相加即可求解.
解答:解:∵四边形ABCD中,∠A=160°,∠B=30°,∠C=60°,
∴∠D=360°-160°-30°-60°=110°,
∴∠1+∠2=360°-(180°-160°)×2=320°,
∠3+∠4=360°-(180°-110°)×2=220°,
∠5+∠6=360°-(180°-60°)×2=120°,
∠7-∠8=-(∠B+∠B′)=-60°,
∴∠1+∠2+∠3+∠4+∠5+∠6+∠7-∠8
=320°+220°+120°-60°
=600°.
故选:A.
∴∠D=360°-160°-30°-60°=110°,
∴∠1+∠2=360°-(180°-160°)×2=320°,
∠3+∠4=360°-(180°-110°)×2=220°,
∠5+∠6=360°-(180°-60°)×2=120°,
∠7-∠8=-(∠B+∠B′)=-60°,
∴∠1+∠2+∠3+∠4+∠5+∠6+∠7-∠8
=320°+220°+120°-60°
=600°.
故选:A.
点评:考查了四边形内角和等于360°,三角形内角和定理,折叠的性质,以及三角形外角的性质的综合应用.

练习册系列答案
相关题目
下列各组数中不能构成直角三角形的一组数是( )
| A、0.3,0.4,0.5 | ||
B、2,2
| ||
| C、5,12,13 | ||
| D、10,11,12 |
| 3 | 8 |
| A、3 | B、2 | C、-2 | D、4 |
下列各式中不是二次根式的为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
下列运算正确的是( )
| A、(-2)3=-6 | ||
B、-1÷2×
| ||
| C、8-5x=3x | ||
| D、-(-2a-5)=2a+5 |
 如图,点P在正方形ABCD内,△PBC是正三角形,BD和PC相交于点E.给出下列结论:
如图,点P在正方形ABCD内,△PBC是正三角形,BD和PC相交于点E.给出下列结论: 如图,点A在反比例函数y=
如图,点A在反比例函数y=