题目内容
16.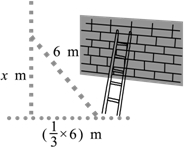 生活表明,靠墙摆放梯子时,若梯子底端离墙的距离为梯子长度的三分之一,则梯子比较稳定.现有一长度为6m的梯子,当梯子稳定摆放时,它的顶端最多能到达多高?(精确到0.1m)
生活表明,靠墙摆放梯子时,若梯子底端离墙的距离为梯子长度的三分之一,则梯子比较稳定.现有一长度为6m的梯子,当梯子稳定摆放时,它的顶端最多能到达多高?(精确到0.1m)
分析 先根据勾股定理求出直角边的长度,再求出答案即可.
解答 解:由勾股定理得:$\sqrt{{6}^{2}-(\frac{1}{3}×6)^{2}}$=$\sqrt{32}$=4$\sqrt{2}$≈5.7,
答:它的顶端最多能到达5.7米高.
点评 本题考查了估算无理数大小,勾股定理的应用,能估算出$\sqrt{2}$的范围是解此题的关键,难度不大.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
7. 如图,若△ABC∽△ACD,∠A=60°,∠ACD=40°,则∠BCD的度数为( )
如图,若△ABC∽△ACD,∠A=60°,∠ACD=40°,则∠BCD的度数为( )
 如图,若△ABC∽△ACD,∠A=60°,∠ACD=40°,则∠BCD的度数为( )
如图,若△ABC∽△ACD,∠A=60°,∠ACD=40°,则∠BCD的度数为( )| A. | 30° | B. | 40° | C. | 50° | D. | 30°或50° |
8.圆内最大的弦长为10cm,则圆的半径( )
| A. | 小于5cm | B. | 大于5cm | C. | 等于5cm | D. | 不能确定 |
5. 如图,在⊙O中,$\widehat{AB}$=2$\widehat{CD}$,则下列结论正确的是( )
如图,在⊙O中,$\widehat{AB}$=2$\widehat{CD}$,则下列结论正确的是( )
 如图,在⊙O中,$\widehat{AB}$=2$\widehat{CD}$,则下列结论正确的是( )
如图,在⊙O中,$\widehat{AB}$=2$\widehat{CD}$,则下列结论正确的是( )| A. | AB>2CD | B. | AB=2CD | C. | AB<2CD | D. | 以上都不正确 |
6.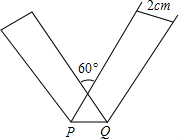 将宽为2cm的长方形纸条折叠成如图的形状,那么折痕PQ的长是( )
将宽为2cm的长方形纸条折叠成如图的形状,那么折痕PQ的长是( )
 将宽为2cm的长方形纸条折叠成如图的形状,那么折痕PQ的长是( )
将宽为2cm的长方形纸条折叠成如图的形状,那么折痕PQ的长是( )| A. | $\frac{2}{3}$$\sqrt{3}$cm | B. | $\frac{4}{3}$$\sqrt{3}$cm | C. | $\sqrt{5}$cm | D. | 2cm |
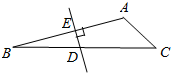 如图所示,在△ABC中,∠C=45°,∠B=15°,AB的垂直平分线交AB于E,交BC于D,DB=10,那么AC=5$\sqrt{2}$.
如图所示,在△ABC中,∠C=45°,∠B=15°,AB的垂直平分线交AB于E,交BC于D,DB=10,那么AC=5$\sqrt{2}$.