题目内容
5.如图,两直线AB、CD相交于点O,OE平分∠BOD,∠AOC:∠AOD=7:11.
(1)求∠COE的度数.
(2)若射线OF⊥OE,请在图中画出OF,并求∠COF的度数.
分析 (1)根据∠AOC+∠AOD=180°可得∠AOC和∠AOD的度数,根据对顶角相等可得∠BOD=70°,再利用角平分线定义可得∠DOE=35°,再根据邻补角定义可得∠COE的度数;
(2)分两种情况画图,进而求出∠COF的度数.
解答 解:(1)∠AOC:∠AOD=7:11,∠AOC+∠AOD=180°,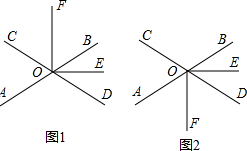
∴∠AOC=70°,∠AOD=110°,
∵∠BOD=∠AOC,
∴∠BOD=70°,
∵OE平分∠BOD,
∴∠DOE=35°,
∴∠COE=180°-∠DOE=145°;
(2)分两种情况,
如图1,∵OF⊥OE,
∴∠EOF=90°,
∴∠COF=∠COE-∠EOF=145°-90°=55°,
如图2,∠COF=∠360°-∠COE-∠EOF=125°.
点评 此题主要考查了垂线、邻补角、对顶角,关键是掌握对顶角相等,邻补角互补.

练习册系列答案
相关题目
10.若一个正多边形的一个外角是36°,则这个正多边形的边数是( )
| A. | 1 0 | B. | 9 | C. | 8 | D. | 6 |
14. 如图,△ABC中,BD平分∠ABC,EF垂直平分BC交BC于点E,交BD于点F,连接CF,若∠A=60°,∠ABD=25°,则∠ACF的度数为( )
如图,△ABC中,BD平分∠ABC,EF垂直平分BC交BC于点E,交BD于点F,连接CF,若∠A=60°,∠ABD=25°,则∠ACF的度数为( )
 如图,△ABC中,BD平分∠ABC,EF垂直平分BC交BC于点E,交BD于点F,连接CF,若∠A=60°,∠ABD=25°,则∠ACF的度数为( )
如图,△ABC中,BD平分∠ABC,EF垂直平分BC交BC于点E,交BD于点F,连接CF,若∠A=60°,∠ABD=25°,则∠ACF的度数为( )| A. | 25° | B. | 45° | C. | 50° | D. | 70° |
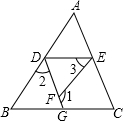 如图,∠1+∠2=180°,∠3=∠B.
如图,∠1+∠2=180°,∠3=∠B. 在平面直角坐标系xOy中,过象限内一点分别作坐标轴的垂线,若与坐标轴围成的矩形的周长与面积相等,则这个点叫做“和谐点”.如图,过点H(-3,6)分别作x轴,y轴的垂线,与坐标轴围成的矩形OAHB的周长与面积相等,则点H(3,6)是“和谐点”.
在平面直角坐标系xOy中,过象限内一点分别作坐标轴的垂线,若与坐标轴围成的矩形的周长与面积相等,则这个点叫做“和谐点”.如图,过点H(-3,6)分别作x轴,y轴的垂线,与坐标轴围成的矩形OAHB的周长与面积相等,则点H(3,6)是“和谐点”. 如图,直线a∥b,将三角尺的直角顶点放在直线b上,∠1=30°,则∠2=60°.
如图,直线a∥b,将三角尺的直角顶点放在直线b上,∠1=30°,则∠2=60°. 如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于F,连接CF.
如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于F,连接CF.