题目内容
12．
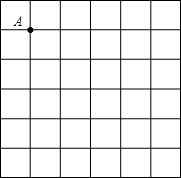作图题：如图，在6×6的正方形网格中，每个小正方形的边长都为1，请在所给网格中按下列要求画出图形．（1）从点A出发的一条线段AB，使它的另一个端点落在格点（即小正方形的顶点）上，且长度为2$\sqrt{2}$；
（2）以（1）中的AB为边的一个等腰三角形ABC，使点C在格点上，且另两边的长都是无理数，请画出所有满足条件的点C；
（3）画出△ABC关于点B的中心对称图形△A1B1C1．
分析 （1）由于AB=2$\sqrt{2}$，则AB为边长为2的正方形的对角线，由此可画出线段AB；
（2）由于△ABC为等腰三角形，且点C在格点上，且另两边的长都是无理数，则C点在AB的垂直平分线上，由此可找出点C；
（3）利用网格特点和旋转的性质画出点A、B、C的对应点A1、B1、C1即可．
解答 解：（1）如图1，线段AB为所作；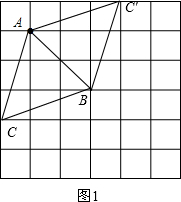
（2）如图1，点C和点C′为所作；
（3）如图2，△A1B1C1为所作．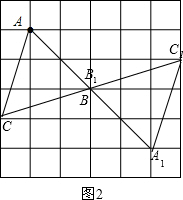
点评 本题考查了作图-旋转变换：根据旋转的性质可知，对应点与旋转中心的连线段的夹角都等于旋转角，对应线段也相等，由此可以通过作相等的角，在角的边上截取相等的线段的方法，找到对应点，顺次连接得出旋转后的图形．也考查了勾股定理．本题属于开放型题型，要读懂题目要求，设计画图方案也比较灵活，培养学生运算能力，动手能力．
练习册系列答案
名校课堂系列答案
相关题目
2．下列方程中，是关于x的一元二次方程为（ ）
| A． | 3x+1=5x+7 | B． | $\frac{1}{{x}^{2}}$+x-1=0 | ||
| C． | x2-5=0 | D． | ax2-bx=5（a和b为常数） |
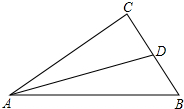
如图，已知：CD=AB，∠BAD=∠BDA，AE是△ABD的中线，求证：AC=2AE．
如图，在△ABC中，∠C=90°，AC=BC，AD平分∠BAC，且CD=1，则△ABD的面积为$\frac{2+\sqrt{2}}{2}$．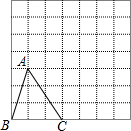
如图：在边长为1个单位长度的小正方形组成的网格中，△ABC的顶点A、B、C在小正方形的顶点上，将△ABC向右平移3单位，再向上平移2个单位得到三角形A1B1C1．