题目内容
3.根据给出的新定义,解答问题.定义:如果两条线段将一个三角形分成3个等腰三角形,我们把这两条线段叫做这个三角形的三分线.如图1所示,BD、CE就是这个三角形的三分线.
(1)在图1中,若AB=2,CD=2-$\sqrt{2}$.
(2)请你在图2中用两种不同的方法画出顶角为36°的等腰三角形的三分线,并标注每个等腰三角形顶角的度数;(若两种方法分得的三角形成3对全等三角形,则视为同一种)
(3)如图3,△ABC中,AC=2,BC=3,∠C=2∠B=2α,请画出△ABC的三分线,并求出两条三分线的长.
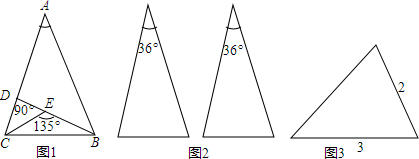
分析 (1)根据△ADB为等腰直角三角形,利用勾股定理求出AD,则CD=AC-AD,即可解答;
(2)根据等腰三角形的判定定理容易画出图形;
(3)根据等腰三角形的判定定理容易画出图形;根据∠B=α,则∠DCB=∠DCA=∠EAC=α,∠ADE=∠AED=2α,则△AEC∽△BDC,△ACD∽△ABC,得出对应边成比例,设AE=AD=x,BD=CD=y,得出方程组,解方程组即可.
解答 解:(1)∵∠CDE=90°,
∴∠ADB=90°,
∴△ADB为等腰直角三角形,
∴AD2+AB2=22.
∴2AD2=4
解得:AD=$\sqrt{2}$,
∵AC=AB=2,
∴CD=AC-AD=$2-\sqrt{2}$.
故答案为:2-$\sqrt{2}$;
(2)如图2作图,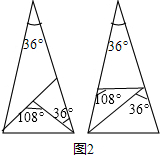
(3)如图3所示,CD、AE就是所求的三分线. 
∵∠B=α,则∠DCB=∠DCA=∠EAC=α,∠ADE=∠AED=2α,
此时△AEC∽△BDC,△ACD∽△ABC,
设AE=AD=x,BD=CD=y,
∵△AEC∽△BDC,
∴x:y=2:3,
∵△ACD∽△ABC,
∴2:x=(x+y):2,
所以联立得方程组$\left\{\begin{array}{l}{x:y=2:3}\\{2:x=(x+y):2}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=\frac{2}{5}\sqrt{10}}\\{y=\frac{3}{5}\sqrt{10}}\end{array}\right.$.
即三分线长分别是$\frac{2}{5}\sqrt{10}$和$\frac{3}{5}\sqrt{10}$.
点评 本题是相似形综合题目,考查了等腰三角形的判定与性质、等腰三角形的画图、相似三角形的判定与性质、解方程组等知识;解决本题的关键是作出图形.

 将长方形ABCD按如图所示沿EF所在直线折叠,点C落在AD上的点C′处,点D落在点D′处.
将长方形ABCD按如图所示沿EF所在直线折叠,点C落在AD上的点C′处,点D落在点D′处. 如图,已知△ABD中,AB=AD=9,BD=3$\sqrt{5}$.
如图,已知△ABD中,AB=AD=9,BD=3$\sqrt{5}$. 如图,已知平面直角坐标系,A,B两点的坐标分别为A(4,-6),B(8,-2).
如图,已知平面直角坐标系,A,B两点的坐标分别为A(4,-6),B(8,-2).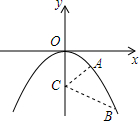 如图所示,在抛物线y=-x2上有A,B两点,其横坐标分别为1,2;在y轴上有一动点C,使AC+BC距离最短,求C点的坐标.
如图所示,在抛物线y=-x2上有A,B两点,其横坐标分别为1,2;在y轴上有一动点C,使AC+BC距离最短,求C点的坐标.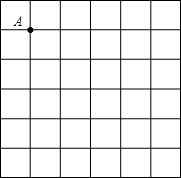 作图题:如图,在6×6的正方形网格中,每个小正方形的边长都为1,请在所给网格中按下列要求画出图形.
作图题:如图,在6×6的正方形网格中,每个小正方形的边长都为1,请在所给网格中按下列要求画出图形. 如图,△ABC的两条高AD、BE相交于点H,且AD=BD,求证:△BDH≌△ADC.
如图,△ABC的两条高AD、BE相交于点H,且AD=BD,求证:△BDH≌△ADC.