Question

1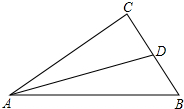．如图，在△ABC中，∠C=90°，AC=BC，AD平分∠BAC，且CD=1，则△ABD的面积为$\frac{2+\sqrt{2}}{2}$．

Answer 1

分析 过点D作DE⊥AB，垂足为E，设AC的边长为a，利用勾股定理和各三角形的面积关系列方程，求出a，即可求得AB的长，再利用三角形面积公式即可求得答案．

解答 解：过点D作DE⊥AB，垂足为E，
设AC的边长为a，则AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{2}$a，
∵S_△ADB=S_△ACB-S_△ACD，
即$\frac{1}{2}$AB×DE=$\frac{1}{2}$a×a-$\frac{1}{2}$a×1，
又∵∠C=90°，AD平分∠BAC，DE⊥AB，
∴CD=DE=1，
∴AB=$\frac{1}{2}$a²-$\frac{1}{2}$a，
∴$\frac{1}{2}$a²-$\frac{1}{2}$a=a$\sqrt{2}$，
解得，a=$\sqrt{2}$+1，
∴AB=a$\sqrt{2}$=2$\sqrt{2}$+$\sqrt{2}$
∴S_△ADB=$\frac{1}{2}$AB×DE=$\frac{1}{2}$×（$\sqrt{2}$+2$\sqrt{2}$）×1=$\frac{2+\sqrt{2}}{2}$．
故答案为：$\frac{2+\sqrt{2}}{2}$．

点评 此题主要考查学生对勾股定理的理解和掌握，解答此题的关键是利用勾股定理和各三角形的面积关系列方程，求出a．此题有一定的拔高难度，属于中档题．