题目内容
14. 如图,在△ABC中,点O是△ABC的外心,过点O作OD⊥AC,交AC于点D,连接BO,过点A作AE⊥BC,垂足为E,若BO=7,OD=3,则cos∠BAE的值为$\frac{2\sqrt{10}}{7}$.
如图,在△ABC中,点O是△ABC的外心,过点O作OD⊥AC,交AC于点D,连接BO,过点A作AE⊥BC,垂足为E,若BO=7,OD=3,则cos∠BAE的值为$\frac{2\sqrt{10}}{7}$.
分析 连接OA、OC,则OA=OC=OA=7,由OD⊥AC,得出∠AOD=∠COD,由勾股定理求出AD,由圆周角定理得出∠ABC=$\frac{1}{2}$∠AOC=∠AOD,得出cos∠BAE=cos∠AOD,即可求出结果.
解答 解:连接OA、OC,如图所示: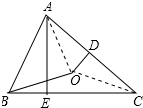
则OA=OC=OA=7,
∵OD⊥AC,
∴∠AOD=∠COD,AD=$\sqrt{O{A}^{2}-O{D}^{2}}$=$\sqrt{{7}^{2}-{3}^{2}}$=2$\sqrt{10}$,
∵点O是△ABC的外心,
∴∠ABC=$\frac{1}{2}$∠AOC=∠AOD,
∴cos∠BAE=cos∠AOD=$\frac{AD}{OA}$=$\frac{2\sqrt{10}}{7}$;
故答案为:$\frac{2\sqrt{10}}{7}$.
点评 本题考查了三角形的外接圆与外心、圆周角定理、勾股定理、等腰三角形的性质、三角函数;熟练掌握圆周角定理,由圆周角定理得出∠ABC=∠AOD是解题的关键.

练习册系列答案
 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案
相关题目
2.娇兰佳人化妆品店为了激发消费者消费,在劳动节当天,对MG面膜进行促销,方案如下:
根据上表中提供的信息,解答下列问题:
(1)若张女士欲购买这款面膜14贴,求她应支付的钱数;
(2)设张女士购买的面膜的数量为x贴,应支付的钱数为y元,请写出y关于x的函数关系式;
(3)若张女士购买面膜的数量为20贴,支付的钱数为y元,当y<170时,求m的取值范围.
| 购买数量(贴) | 单价(元/贴) |
| 不超过10贴(包含10贴) | 9 |
| 超过10贴不超过m贴的部分(15≤m≤30) | 8 |
| 超过m贴的部分 | 7 |
(1)若张女士欲购买这款面膜14贴,求她应支付的钱数;
(2)设张女士购买的面膜的数量为x贴,应支付的钱数为y元,请写出y关于x的函数关系式;
(3)若张女士购买面膜的数量为20贴,支付的钱数为y元,当y<170时,求m的取值范围.
9.已知关于x的不等式x<2x-3的解可以使不等式x+2(x-3)>m成立,则m的取值范围是( )
| A. | m≤3 | B. | m<3 | C. | m≥3 | D. | m<-3 |
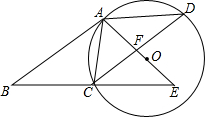 如图,在?ABCD中,AC=AD,⊙O是△ACD的外接圆,BC的延长线与AO的延长线交干E.
如图,在?ABCD中,AC=AD,⊙O是△ACD的外接圆,BC的延长线与AO的延长线交干E. 如图,小明用长为3m的竹竿CD做测量工具,测量学校旗杆AB的高度,移动竹竿,使竹竿与旗杆的顶端C、A与O点在一条直线上,则根据图中数据可得旗杆AB的高为9m.
如图,小明用长为3m的竹竿CD做测量工具,测量学校旗杆AB的高度,移动竹竿,使竹竿与旗杆的顶端C、A与O点在一条直线上,则根据图中数据可得旗杆AB的高为9m. 如图,在Rt△ABC中,∠ACB=90°,CD是AB边长的中线,若AC=6,BC=8,则CD的长是( )
如图,在Rt△ABC中,∠ACB=90°,CD是AB边长的中线,若AC=6,BC=8,则CD的长是( )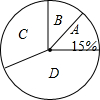 京东商城在2014年的春节前期,空调、冰箱、彩电和洗衣机这四种家电的销售情况如图所示,其中A表示空调、B表示冰箱、C表示彩电、D表示洗衣机,冰箱、彩电和洗衣机的销售量之比为6:20:25.若冰箱售出12万台,则这四种家电总共销售120万台.
京东商城在2014年的春节前期,空调、冰箱、彩电和洗衣机这四种家电的销售情况如图所示,其中A表示空调、B表示冰箱、C表示彩电、D表示洗衣机,冰箱、彩电和洗衣机的销售量之比为6:20:25.若冰箱售出12万台,则这四种家电总共销售120万台.