题目内容
4．解分式方程：$\frac{3}{x-1}$+1=$\frac{{x}^{2}}{{x}^{2}-1}$．分析 分式方程去分母转化为整式方程，求出整式方程的解得到x的值，经检验即可得到分式方程的解．
解答 解：去分母得：3（x+1）+x2-1=x2，
整理得：3x+3-1=0，
解得：x=-$\frac{2}{3}$，
经检验x=-$\frac{2}{3}$是分式方程的解．
点评 此题考查了解分式方程，解分式方程的基本思想是“转化思想”，把分式方程转化为整式方程求解．解分式方程一定注意要验根．
练习册系列答案
相关题目
17．
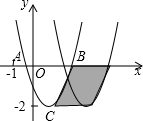如图，已知抛物线y=ax2+bx+c与轴交于A、B两点，顶点C的纵坐标为-2，现将抛物线向右平移2个单位，得到抛物线y=a1x2+b1x+c1，则下列结论：
①b＞0；②a-b+c＜0；③阴影部分的面积为4；④若c=-1，则b2=4a．
正确的是（ ）
如图，已知抛物线y=ax2+bx+c与轴交于A、B两点，顶点C的纵坐标为-2，现将抛物线向右平移2个单位，得到抛物线y=a1x2+b1x+c1，则下列结论：①b＞0；②a-b+c＜0；③阴影部分的面积为4；④若c=-1，则b2=4a．
正确的是（ ）
| A． | ①③ | B． | ②③ | C． | ②④ | D． | ③④ |
19．
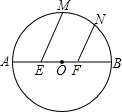如图，已知⊙O的直径AB=12，E、F为AB的三等分点，M、N为$\widehat{AB}$上两点，且∠MEB=∠NFB=60°，则EM+FN=（ ）
如图，已知⊙O的直径AB=12，E、F为AB的三等分点，M、N为$\widehat{AB}$上两点，且∠MEB=∠NFB=60°，则EM+FN=（ ）| A． | $\frac{\sqrt{33}}{2}$ | B． | $\sqrt{33}$ | C． | 2$\sqrt{33}$ | D． | 33 |
9．
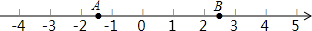如图，数轴上两点A、B表示的数可能是（ ）
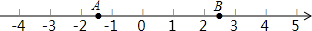如图，数轴上两点A、B表示的数可能是（ ）| A． | -1.5和2.5 | B． | -2.5和2.5 | C． | -1.5和3.5 | D． | -2.5和3.5 |
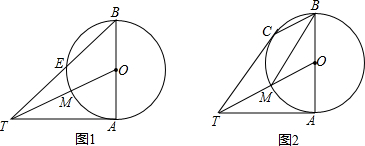
如图，在△ABC中，点O是△ABC的外心，过点O作OD⊥AC，交AC于点D，连接BO，过点A作AE⊥BC，垂足为E，若BO=7，OD=3，则cos∠BAE的值为$\frac{2\sqrt{10}}{7}$．