题目内容
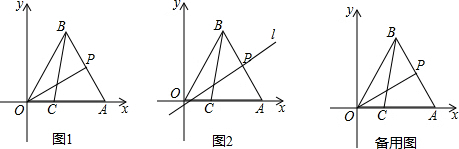
4.如图1,在平面直角坐标系中,△OAB是等边三角形,O为坐标原点,点A的坐标是(3,0),点C在OA上且OC=1,连接BC.一动点P从点A出发,沿折线A→B→O的方向向终点O运动,记点P移动的路程为m.(1)当点P在线段AB上运动时,连接OP,求满足△BPO≌△OCB的m值;
(2)连接PC,求△OPC的面积s关于m的函数表达式;
(3)如图2,过点P作边AB的垂线l,并以直线l为对称轴,作线段AC的对称线段A1C1.请写出在点P的运动过程中,线段A1C1与y轴有交点时m的取值范围.
分析 (1)由全等三角形的性质可知BP=OC,由m=AB-PB求解即可;
(2)过点P作PD⊥OA,垂足为D,三角形OPC的面积S=$\frac{1}{2}$OC•DP,然后分为点P在AB和OB上两种情况求得PD的长,从而得到S与m的函数关系式;
(3)求得点A′或点C′恰好在y轴上时m的值,从而可确定出m的范围.
解答 解:(1)∵△BPO≌△OCB,
∴BP=OC=1.
∴m=AB-BP=3-1=2.
(2)①如图1所示:当点P在AB上运动时,过点P作PD⊥OA.
∵∠OAP=60°,∠PDA=90°,
∴∠APD=30°.
∴PD=$\frac{\sqrt{3}}{2}$PA$\frac{\sqrt{3}}{2}$m.
∴S=$\frac{1}{2}$×1×$\frac{{\sqrt{3}}}{2}$m=$\frac{{\sqrt{3}}}{4}$m;
②如图2所示:当点P在OB上时,过点P作PD⊥OA.
∵OP=AB+OB-m=6-m,
∴PD=$\frac{{\sqrt{3}}}{2}$(6-m),
∴S=$\frac{1}{2}$×1×$\frac{{\sqrt{3}}}{2}$(6-m)=$\frac{{\sqrt{3}}}{4}$(6-m).
综上所述,S与m的函数关系式为S=$\left\{\begin{array}{l}{\frac{\sqrt{3}}{4}m(0<m≤3)}\\{\frac{\sqrt{3}}{4}(6-m)(3<m<6)}\end{array}\right.$.
(3)如图3所示:当点C的对应点C′落在y轴上时.
由翻折的性质可知:CC′⊥PE,DC=DC′,
又∵PE⊥AB,
∴DC∥PA.
∴∠C′CO=∠A=60°.
∴∠CC′O=30°.
∴CC′=2OC=2.
∴DC=1.
∵在△DCE中,∠EDC=90°,∠DCE=60°,
∴∠DEC=30°.
∴EC=2DC=2.
∴EC=CA.
∵DC∥AB,
∴$\frac{DC}{AP}=\frac{EC}{AE}$=$\frac{1}{2}$.
∴AP=2.即m=2.
如图4所示:当点A的对称点A′在y轴上时.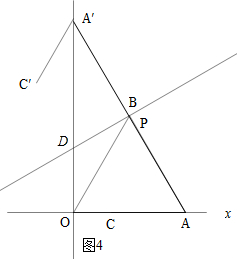
∵点A与点A′关于直线PD对称,
∴PA=PA′.
∵∠A=60°,∠AOA′=90°,
∴∠AA′O=30°.
∴AA′=2OA=6.
∴PA=3.
∴点B与点P重合,此时m=3.
如图5所示:当点P在OB上,点C′在y轴上.
∵∠PCO=60°,∠POC=60°,
∴△OPC为等边三角形.
∴PO=OC=1.
∴PB=2.
∴m=PB+AB=5.
∴线段A1C1与y轴有交点时m的取值范围是2≤m≤5.
点评 本题主要考查的是一次函数的综合应用,解答本题主要应用了全等三角形的性质和判定、等边三角形的性质、翻折的性质,三角形的面积公式,求得点A′和点C′恰好在y轴上时m的值是解题的关键.

 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案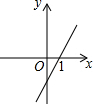 已知一次函数y=kx+b的图象如图所示,则下列语句中不正确的是( )
已知一次函数y=kx+b的图象如图所示,则下列语句中不正确的是( )| A. | 函数值y随x的增大而增大 | B. | 当x>0时,y>0 | ||
| C. | k+b=0 | D. | kb<0 |
| A. | $\frac{23}{3}$ | B. | $\sqrt{1}$ | C. | 1.101001 | D. | -π |
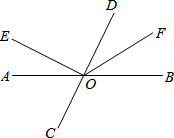 如图,直线AB,CD相交于点O,OE⊥CD,OF平分∠BOD,若∠AOE=26°,求∠COF的度数.
如图,直线AB,CD相交于点O,OE⊥CD,OF平分∠BOD,若∠AOE=26°,求∠COF的度数.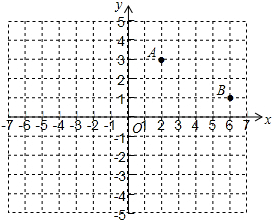 如图,在平面直角坐标系中,已知点A(2,3),点B(6,1)关于y轴对称的点分别是点C,点D.
如图,在平面直角坐标系中,已知点A(2,3),点B(6,1)关于y轴对称的点分别是点C,点D. 如图,A、D、F、B在同一直线上,AD=BF,AE=BC,∠A=∠B,求证:△AEF≌△BCD.
如图,A、D、F、B在同一直线上,AD=BF,AE=BC,∠A=∠B,求证:△AEF≌△BCD.