题目内容
14.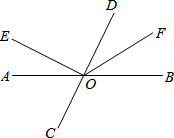 如图,直线AB,CD相交于点O,OE⊥CD,OF平分∠BOD,若∠AOE=26°,求∠COF的度数.
如图,直线AB,CD相交于点O,OE⊥CD,OF平分∠BOD,若∠AOE=26°,求∠COF的度数.
分析 首先根据垂直的定义和∠AOE的度数求得∠DOB的度数,然后根据角平分线的定义求得∠DOF的度数,从而根据平角的定义求得∠COF的度数即可.
解答 解:∵OE⊥CD,
∴∠EOD=90°,
∵∠AOE=26°,
∴∠DOB=180°-∠AOE-∠EOD=64°,
∵OF平分∠BOD,
∴∠DOF=$\frac{1}{2}$∠DOB=32°,
∴∠COF=180°-∠DOF=148°.
点评 此题考查的知识点是垂线、角的计算及对顶角知识,关键是根据垂线、角平分线定义得出所求角与已知角的关系转化求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5. 如图,?ABCD中,∠B=70°,点E是BC的中点,点F在AB上,且BF=BE,过点F作FG⊥CD于点G,有如下结论:①AF=CG;②∠EFG=35°;③CE=DG;④∠FEG=100°;⑤∠EGC=55°;其中正确的有( )
如图,?ABCD中,∠B=70°,点E是BC的中点,点F在AB上,且BF=BE,过点F作FG⊥CD于点G,有如下结论:①AF=CG;②∠EFG=35°;③CE=DG;④∠FEG=100°;⑤∠EGC=55°;其中正确的有( )
 如图,?ABCD中,∠B=70°,点E是BC的中点,点F在AB上,且BF=BE,过点F作FG⊥CD于点G,有如下结论:①AF=CG;②∠EFG=35°;③CE=DG;④∠FEG=100°;⑤∠EGC=55°;其中正确的有( )
如图,?ABCD中,∠B=70°,点E是BC的中点,点F在AB上,且BF=BE,过点F作FG⊥CD于点G,有如下结论:①AF=CG;②∠EFG=35°;③CE=DG;④∠FEG=100°;⑤∠EGC=55°;其中正确的有( )| A. | ①②③ | B. | ①②③⑤ | C. | ①③④⑤ | D. | ②⑤ |
9.去年我省规划重建校舍约3876000平方米,这个数精确到十万位并用科学记数法表示为( )
| A. | 3.8×106平方米 | B. | 3.8×107平方米 | C. | 3.9×106平方米 | D. | 3.9×107平方米 |
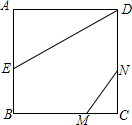 如图,正方形ABCD的边长为4,AE=EB,MN=2,线段MN的两端在CB、CD上滑动,当CM=$\frac{2\sqrt{5}}{5}$或$\frac{\sqrt{5}}{5}$时,△ADE与△CMN相似.
如图,正方形ABCD的边长为4,AE=EB,MN=2,线段MN的两端在CB、CD上滑动,当CM=$\frac{2\sqrt{5}}{5}$或$\frac{\sqrt{5}}{5}$时,△ADE与△CMN相似.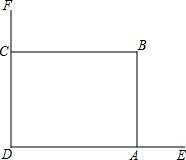 在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角,墙DF足够长,墙DE长为12米,现用20米长的篱笆围成一个矩形花园ABCD,点C在墙DF上,点A在墙DE上,(篱笆只围AB,BC两边).
在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角,墙DF足够长,墙DE长为12米,现用20米长的篱笆围成一个矩形花园ABCD,点C在墙DF上,点A在墙DE上,(篱笆只围AB,BC两边).