题目内容
12．
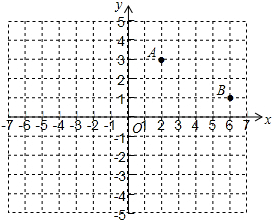如图，在平面直角坐标系中，已知点A（2，3），点B（6，1）关于y轴对称的点分别是点C，点D．（1）请写出点C，点D的坐标；
（2）在x轴上求作一点P，使PA+PB的值最小（保留作图痕迹，不要求写作法）并直接写出点P的坐标．
分析 （1）关于y轴对称的两点的横坐标互为相反数，纵坐标相等；
（2）首先求得点A关于x轴的对称点A′，连接A′B交x轴于点P，此时PA+PB的值最小．
解答 解：（1）点C的坐标为（-2，3），点D的坐标为（-6，1）；
（2）如图所示：
根据图形可知点P的坐标为（5，0）．
点评 本题主要考查的是轴对称图形的性质、轴对称--路径最短问题，掌握轴对称图形的性质是解题的关键．
练习册系列答案
世纪百通期末金卷系列答案
相关题目
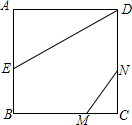如图，正方形ABCD的边长为4，AE=EB，MN=2，线段MN的两端在CB、CD上滑动，当CM=$\frac{2\sqrt{5}}{5}$或$\frac{\sqrt{5}}{5}$时，△ADE与△CMN相似．
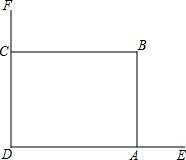在美化校园的活动中，某兴趣小组想借助如图所示的直角墙角，墙DF足够长，墙DE长为12米，现用20米长的篱笆围成一个矩形花园ABCD，点C在墙DF上，点A在墙DE上，（篱笆只围AB，BC两边）．
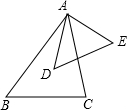如图，若∠BAD=∠CAE，∠E=∠C，则△ABC∽△ADE．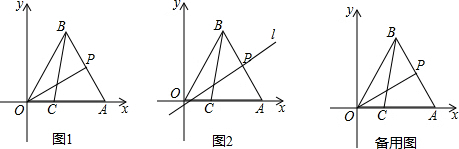
17．已知点P的坐标为（3，-2），则点P到y轴的距离为（ ）
| A． | 3 | B． | 2 | C． | 1 | D． | 5 |
如图，两个正方形边长分别为a、b，如果a+b=18，ab=60，求图中阴影部分的面积．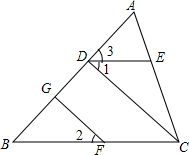
∠1=∠2，∠3=∠B，FG⊥AB于G，猜想CD与AB的关系，并证明你的猜想．