题目内容
11.两位同学在解方程组时,甲同学由$\left\{\begin{array}{l}{ax+by=2}\\{cx-7y=8}\end{array}\right.$正确地解出$\left\{\begin{array}{l}{x=3}\\{y=-2}\end{array}\right.$,乙同学因把C写错了解得 $\left\{\begin{array}{l}x=-2\\ y=2\end{array}\right.$,那么a、b、c的正确的值应为多少?分析 把$\left\{\begin{array}{l}{x=3}\\{y=-2}\end{array}\right.$代入$\left\{\begin{array}{l}{ax+by=2}\\{cx-7y=8}\end{array}\right.$得:$\left\{\begin{array}{l}{3a-2b=2}\\{3c+14=8}\end{array}\right.$,把 $\left\{\begin{array}{l}x=-2\\ y=2\end{array}\right.$代入ax+by=2得:-2a+2b=2,组成方程组$\left\{\begin{array}{l}{3a-2b=2}\\{3c+14=8}\\{-2a+2b=2}\end{array}\right.$,解方程组即可.
解答 解:把$\left\{\begin{array}{l}{x=3}\\{y=-2}\end{array}\right.$代入$\left\{\begin{array}{l}{ax+by=2}\\{cx-7y=8}\end{array}\right.$得:$\left\{\begin{array}{l}{3a-2b=2}\\{3c+14=8}\end{array}\right.$,
把 $\left\{\begin{array}{l}x=-2\\ y=2\end{array}\right.$代入ax+by=2得:-2a+2b=2,
∴$\left\{\begin{array}{l}{3a-2b=2}\\{3c+14=8}\\{-2a+2b=2}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=4}\\{b=5}\\{c=-2}\end{array}\right.$.
点评 本题考查了二元一次方程组的解,解决本题的关键是组成三元一次方程组.

 提分百分百检测卷系列答案
提分百分百检测卷系列答案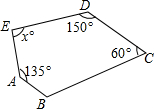 如图,若AB∥CD,则∠E的度数为( )
如图,若AB∥CD,则∠E的度数为( )| A. | 60° | B. | 65° | C. | 70° | D. | 75° |
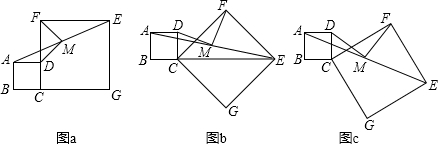
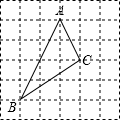 如图,三角形ABC在正方形网格中(图中每个小正方形的边长均为1个单位长度),若点A的坐标为(0,3),点B的坐标为(-2,-1),按要求解下列问题:
如图,三角形ABC在正方形网格中(图中每个小正方形的边长均为1个单位长度),若点A的坐标为(0,3),点B的坐标为(-2,-1),按要求解下列问题: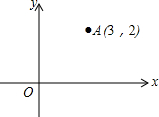 如图,在平面直角坐标系中,点A的坐标为(3,2),能否建立一个新的平面直角坐标系x′O′y′,使得在新的x′O′y′中,点O的坐标变为(-3,-2)?如果可以,请画出新的坐标系;若不可以,请说明理由.
如图,在平面直角坐标系中,点A的坐标为(3,2),能否建立一个新的平面直角坐标系x′O′y′,使得在新的x′O′y′中,点O的坐标变为(-3,-2)?如果可以,请画出新的坐标系;若不可以,请说明理由.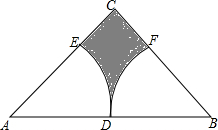 如图,在等腰直角三角形ABC中,∠C=90°,点D为AB的中点,已知扇形EAD和扇形FBD的圆心分别为点A、点B,且AB=4,则图中阴影部分的面积为4-π(结果保留π).
如图,在等腰直角三角形ABC中,∠C=90°,点D为AB的中点,已知扇形EAD和扇形FBD的圆心分别为点A、点B,且AB=4,则图中阴影部分的面积为4-π(结果保留π).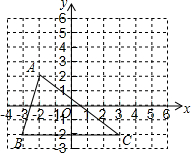 如图,在平面直角坐标系中,A(-2,2)、B(-3,-2)、C(3,-2)
如图,在平面直角坐标系中,A(-2,2)、B(-3,-2)、C(3,-2)