题目内容
1．
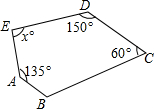如图，若AB∥CD，则∠E的度数为（ ）| A． | 60° | B． | 65° | C． | 70° | D． | 75° |
分析 根据平行线的性质求出∠B，根据多边形的内角和定理得出∠E=（5-2）×180°-∠A-∠B-∠C-∠D，代入求出即可．
解答 解：∵AB∥CD，
∴∠B+∠C=180°，
∵∠C=60°，
∴∠B=120°，
∵∠A=135°，∠D=150°，
∴∠E=（5-2）×180°-∠A-∠B-∠C-∠D=75°，
故选D．
点评 本题考查了多边形的内角和定理，平行线的性质的应用，解此题的关键是求出∠E=（5-2）×180°-∠A-∠B-∠C-∠D和求出∠B+∠C=180°，注意：两直线平行，同旁内角互补．
练习册系列答案
相关题目
9．近年来，我国持续大面积的雾霾天气让环保和健康问题成为全社会关注的焦点．为进一步普及环保和健康知识，某初中学校进行了“关注环境•保护环境”的知识竞赛，参加决赛的15名选手的成绩统计见下表，则参加决赛的选手的成绩的众数和中位数是（ ）
| 成绩 | 60 | 70 | 80 | 90 | 100 |
| 人数 | 3 | 4 | 5 | 2 | 1 |
| A． | 70分，80分 | B． | 70分，70分 | C． | 80分，80分 | D． | 80分，90分 |
10．下列方程中有解的是（ ）
| A． | x2+x-1=0 | B． | x2+x+1=0 | C． | |x|=-1 | D． | $\frac{x-1}{x+2}$=$\frac{x-3}{2+x}$ |