题目内容

1．在平面直角坐标系中，不管实数a取什么实数，抛物线y=ax2+2x+3的顶点都在同一条直线上，这条直线的函数关系式是y=x+3．

分析 求得抛物线y=ax2+2x+3的顶点的横坐标x=-$\frac{b}{2a}$=-$\frac{2}{2a}$-$\frac{1}{a}$，纵坐标y=$\frac{4ac-{b}^{2}}{4a}$=$\frac{12a-4}{4a}$=3-$\frac{1}{a}$，即可得出纵坐标和横坐标的关系式．

解答 解：抛物线y=ax2+2x+3的顶点的横坐标x=-$\frac{b}{2a}$=-$\frac{2}{2a}$-$\frac{1}{a}$，纵坐标y=$\frac{4ac-{b}^{2}}{4a}$=$\frac{12a-4}{4a}$=3-$\frac{1}{a}$，
∴y=x+3，
∴这条直线的函数关系式为y=x+3．
故答案为y=x+3．

点评 本题考查了二次函数的性质，熟练掌握抛物线顶点坐标公式是解题的关键．

练习册系列答案
相关题目
11．符号$|\begin{array}{l}{a}&{b}\\{c}&{d}\end{array}|$称为二阶行列式，规定它的运算法则为$|\begin{array}{l}{a}&{b}\\{c}&{d}\end{array}|$=ad-bc，例如：$|\begin{array}{l}{3}&{5}\\{4}&{7}\end{array}|$=3×7-4×5=21-20=1．请你根据阅读材料化简下面的二阶行列式：$|\begin{array}{l}{2a-1}&{3a+5}\\{a-5}&{2a+1}\end{array}|$，并求当a=-5时，该二阶行列式的值．
12．如图，在平面直角坐标系中，A（-2，2），B（-3，-2）
（1）若点D与点A关于y轴对称，则点D的坐标为（2，2）．
（2）将点B先向右平移5个单位再向上平移1个单位得到点C，则点C的坐标为（2，1）．
（3）求A，B，C，D组成的四边形ABCD的面积．
9．若x=$\sqrt{2}$+1，则x3-（2+$\sqrt{2}$）x2+（1+2$\sqrt{2}$）x-$\sqrt{2}$的值是2．
16．已知55=3125，56=15625，57=78125，58=390625，…，则52013的末4位数是3125．
6．如图，已知：AC、BD相交于E，DE=CE，∠BAC=∠ABD，则图中有2个等腰三角形，3对全等三角形．
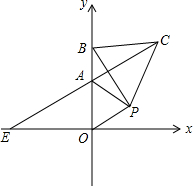13．如图，在平面直角坐标系中，△AOP为等边三角形，A（0，a），P（b，c），且（a-2）2+|b-$\sqrt{3}$|+c2-2c+1=0，点B为y轴上一动点，以BP为边作等边三角形△PBC．
（1）求证：OB=AC；
（2）求a，b，c的值；
（3）当点B运动时，AE的长度是否发生变化？为什么？
（4）在x轴上是否存在点F，使得△OPF是等腰三角形？若存在，求出F点坐标；若不存在，说明理由．
10．下列说法错误的是（　　）
A．-1的立方根是-1B．1的平方根是1C．$\sqrt{2}$是2的平方根D．-3是9的平方根
11．去括号a-（b-2）=a-b+2．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网