题目内容
13.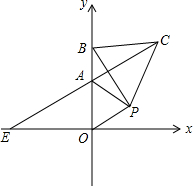 如图,在平面直角坐标系中,△AOP为等边三角形,A(0,a),P(b,c),且(a-2)2+|b-$\sqrt{3}$|+c2-2c+1=0,点B为y轴上一动点,以BP为边作等边三角形△PBC.
如图,在平面直角坐标系中,△AOP为等边三角形,A(0,a),P(b,c),且(a-2)2+|b-$\sqrt{3}$|+c2-2c+1=0,点B为y轴上一动点,以BP为边作等边三角形△PBC.(1)求证:OB=AC;
(2)求a,b,c的值;
(3)当点B运动时,AE的长度是否发生变化?为什么?
(4)在x轴上是否存在点F,使得△OPF是等腰三角形?若存在,求出F点坐标;若不存在,说明理由.
分析 (1)由等边三角形的性质可知:PA=OP,PB=PC,然后再证明∠OPB=∠APC,依据SAS证明△OPB≌△APC,从而得到OB=AC;
(2)将c2-2c+1变形为(c-1)2,然后依据非负数的性质求解即可;
(3)由△OPB≌△APC可知∠APC=60°,从而可知AE的长度不会变化;
(4)分别以点O,P,F为顶点进行分类讨论即可.
解答 解:(1)∵△AOP、△PBC是等边三角形,
∴PA=OP,PB=PC,∠OPA=∠BPC=60°.
∴∠OPA+∠APB=∠BPC+∠APB,即∠OPB=∠APC.
在△OPB和△APC中,
$\left\{\begin{array}{l}{PA=OP}\\{∠OPB=∠APC}\\{PB=PC}\end{array}\right.$,
∴△OPB≌△APC.
∴OB=AC.
(2)∵(a-2)2+|b-$\sqrt{3}$|+c2-2c+1=0,
∴(a-2)2+|b-$\sqrt{3}$|+(c-1)2=0.
∴a=2,b=$\sqrt{3}$,c=1.
(3)∵△OPB≌△APC,
∴∠BOP=∠CAP=60°.
∴∠CAO=120°.
∵∠CAO为定值,
∴AE的长度不会变化.
(4)如图1所示:PO=PF,过点P作PD⊥OF.
∵OP=PF,PD⊥OF,
∴OD=DF.
∵∠POD=30°,PD⊥OD,
∴OD=OP×$\frac{\sqrt{3}}{2}$=$\sqrt{3}$.
∴OF=2$\sqrt{3}$.
∴点F的坐标为(2$\sqrt{3}$,0).
如图2所示:OP=OF.
∵OP=OF=2,
∴点F的坐标为(2,0)或(-2,0).
如图3所示:OF=FP,过点F作FD⊥OP.
∵OF=FP,FD⊥OP,
∴OD=$\frac{1}{2}$OP=1.
在Rt△ODF中,OF=DO$÷\frac{\sqrt{3}}{2}$=1×$\frac{2}{\sqrt{3}}$=$\frac{2\sqrt{3}}{3}$.
∴点F的坐标为($\frac{2\sqrt{3}}{3}$,0).
综上所述,点F的坐标为(2$\sqrt{3}$,0)或(2,0)或($\frac{2\sqrt{3}}{3}$,0)或(-2,0).
点评 本题主要考查的是等边三角形的性质、全等三角形的性质和判定、等腰三角形的性质,根据题意画出图形是解题的关键.

 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案| A. | 12次 | B. | 11次 | C. | 6次 | D. | 5次 |
 如图,在△ABC中,AB=AC,∠BAC=120°,D、F分别为AB、AC的中点,且DE⊥AB,FG⊥AC,点E、G在BC上,BC=18cm,求线段EG的长.(提示:需要添加辅助线)
如图,在△ABC中,AB=AC,∠BAC=120°,D、F分别为AB、AC的中点,且DE⊥AB,FG⊥AC,点E、G在BC上,BC=18cm,求线段EG的长.(提示:需要添加辅助线)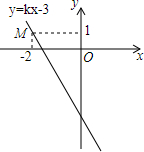 如图,已知直线y=kx-3经过点M,求此直线与x轴,y轴形成的三角形的面积.
如图,已知直线y=kx-3经过点M,求此直线与x轴,y轴形成的三角形的面积.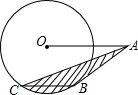 如图,⊙O的半径为4,OA=8,AB切⊙O于B,弦BC∥OA,连接AC,则图中阴影部分的面积为$\frac{8}{3}$π.
如图,⊙O的半径为4,OA=8,AB切⊙O于B,弦BC∥OA,连接AC,则图中阴影部分的面积为$\frac{8}{3}$π.