题目内容
9.若x=$\sqrt{2}$+1,则x3-(2+$\sqrt{2}$)x2+(1+2$\sqrt{2}$)x-$\sqrt{2}$的值是2.分析 首先去括号,进而重新分组分解因式,再将已知代入求出答案.
解答 解:x3-(2+$\sqrt{2}$)x2+(1+2$\sqrt{2}$)x-$\sqrt{2}$
=x3-2x2-$\sqrt{2}$x2+x+2$\sqrt{2}$x-$\sqrt{2}$
=(x3-2x2+x)-($\sqrt{2}$x2-2$\sqrt{2}$x+$\sqrt{2}$)
=x(x-1)2-$\sqrt{2}$(x-1)2
=(x-$\sqrt{2}$)(x-1)2,
将x=$\sqrt{2}$+1,代入上式可得:
原式=($\sqrt{2}$+1-$\sqrt{2}$)($\sqrt{2}$+1-1)2
=2.
点评 此题主要考查了因式分解的应用,正确进行分解因式是解题关键.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
20. 如图,AB∥CD,∠DBF=110°,∠ECD=70°,则∠E的度数为( )
如图,AB∥CD,∠DBF=110°,∠ECD=70°,则∠E的度数为( )
 如图,AB∥CD,∠DBF=110°,∠ECD=70°,则∠E的度数为( )
如图,AB∥CD,∠DBF=110°,∠ECD=70°,则∠E的度数为( )| A. | 30° | B. | 40° | C. | 50° | D. | 60° |
 如图,在△ABC中,AB=AC,∠BAC=120°,D、F分别为AB、AC的中点,且DE⊥AB,FG⊥AC,点E、G在BC上,BC=18cm,求线段EG的长.(提示:需要添加辅助线)
如图,在△ABC中,AB=AC,∠BAC=120°,D、F分别为AB、AC的中点,且DE⊥AB,FG⊥AC,点E、G在BC上,BC=18cm,求线段EG的长.(提示:需要添加辅助线)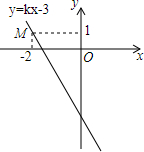 如图,已知直线y=kx-3经过点M,求此直线与x轴,y轴形成的三角形的面积.
如图,已知直线y=kx-3经过点M,求此直线与x轴,y轴形成的三角形的面积.