题目内容
7.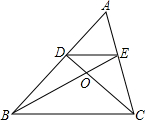 如图,已知点D、E分别在边AB、AC上,BE、CD交于点O,$\frac{AE}{AC}$=$\frac{DE}{BC}$=$\frac{EO}{BO}$.AC=5,EC=3,BC=6,BE=7
如图,已知点D、E分别在边AB、AC上,BE、CD交于点O,$\frac{AE}{AC}$=$\frac{DE}{BC}$=$\frac{EO}{BO}$.AC=5,EC=3,BC=6,BE=7(1)求DE、EO的长;
(2)若△BOC的面积为15,求△ABC的面积.
分析 (1)根据AC=5,EC=3,求得AE=2,根据已知条件求得$\frac{AE}{AC}=\frac{DE}{BC}$=$\frac{2}{5}$,由于BC=6,于是得到DE=$\frac{12}{5}$,由于$\frac{DE}{BC}=\frac{EO}{BO}$=$\frac{2}{5}$,即可得到结果;
(2)由于$\frac{BE}{BO}$=$\frac{7}{5}$,于是得到$\frac{{S}_{△BCE}}{{S}_{△BOC}}$=$\frac{7}{5}$,根据△BOC的面积为15,求得S△BCE=21,由于$\frac{AE}{CE}=\frac{2}{3}$,于是得到$\frac{{S}_{△ABE}}{{S}_{△BCE}}$=$\frac{2}{3}$,求出S△ABE=14,即可得到结论.
解答 解:(1)∵AC=5,EC=3,
∴AE=2,
∵$\frac{AE}{AC}=\frac{DE}{BC}$=$\frac{2}{5}$,
∵BC=6,
∴DE=$\frac{12}{5}$,
∵$\frac{DE}{BC}=\frac{EO}{BO}$=$\frac{2}{5}$,
∵BE=7,
∴EO=2;
(2)∵$\frac{BE}{BO}$=$\frac{7}{5}$,
∴$\frac{{S}_{△BCE}}{{S}_{△BOC}}$=$\frac{7}{5}$,
∵△BOC的面积为15,
∴S△BCE=21,
∵$\frac{AE}{CE}=\frac{2}{3}$,
∴$\frac{{S}_{△ABE}}{{S}_{△BCE}}$=$\frac{2}{3}$,
∴S△ABE=14,
∴△ABC的面积=S△BCE+S△ABE=35.
点评 本题考查了三角形的面积的求法,熟练掌握等高不等底的三角形的面积的比等于底的比是解题的关键.

 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案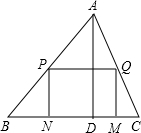 一块材料的形状是锐角三角形ABC,边BC=12cm,高AD=8cm,把它加工成矩形零件如图,要使矩形的一边在BC上,其余两个顶点分别在AB,AC上.且矩形的长与宽的比为3:2,求这个矩形零件的边长.
一块材料的形状是锐角三角形ABC,边BC=12cm,高AD=8cm,把它加工成矩形零件如图,要使矩形的一边在BC上,其余两个顶点分别在AB,AC上.且矩形的长与宽的比为3:2,求这个矩形零件的边长.
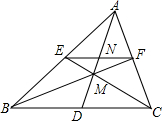 如图,E、F分别在△ABC的边AC、AB上,EF∥BC,BE与CF相交于M,AM交BC于D,交EF于N,求证:BD=DC.
如图,E、F分别在△ABC的边AC、AB上,EF∥BC,BE与CF相交于M,AM交BC于D,交EF于N,求证:BD=DC.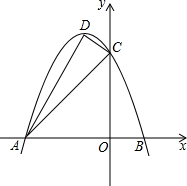 已知抛物线y=ax2+bx+c的对称轴为x=-1,与x轴交于 A(-3,0)、B两点,与y轴交于点C(0,3),顶点为D,连接AC、CD、AD.
已知抛物线y=ax2+bx+c的对称轴为x=-1,与x轴交于 A(-3,0)、B两点,与y轴交于点C(0,3),顶点为D,连接AC、CD、AD.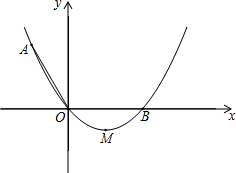 如图,在平面直角坐标系xOy中,抛物线y=ax2+bx(a>0)经过点A和x轴正半轴上的点B,顶点为M且AO=0B=2,∠AOB=120°.
如图,在平面直角坐标系xOy中,抛物线y=ax2+bx(a>0)经过点A和x轴正半轴上的点B,顶点为M且AO=0B=2,∠AOB=120°.