题目内容
11. 如图所示,点A为∠MON的角平分线上一点,过A任作一直线分别与∠MON的两边交于B、C,P为BC的中点,过P作BC的垂线交OA于点D.∠MON=50°,则∠BDC=( )
如图所示,点A为∠MON的角平分线上一点,过A任作一直线分别与∠MON的两边交于B、C,P为BC的中点,过P作BC的垂线交OA于点D.∠MON=50°,则∠BDC=( )| A. | 120° | B. | 130° | C. | 140° | D. | 150° |
分析 过点D作DE⊥OM于点E,作DF⊥ON于点F,证明△DEB≌△DFC,然后得出∠OBD与∠DCO互补,进而得到∠MON与∠BDC互补.
解答 解:过点D作DE⊥OM于点E,作DF⊥ON于点F,如图,
∵P为BC的中点,且DP⊥BC,
∴DB=DC,
∵OD平分∠MON,
∴DE=DF,
在Rt△DEB和Rt△DFC中,
$\left\{\begin{array}{l}{DE=DF}\\{DB=DC}\end{array}\right.$,
∴Rt△DEB≌Rt△DFC(HL),
∴∠DCF=∠DBE,
∵∠DBE+∠OBD=180°
∴∠DCF+∠OBD=180°,
∴∠MON+∠BDC=180°,
∵∠MON=50°,
∴∠BDC=130°.
点评 本题主要考查了角平分线的性质、全等三角形的判定与性质、等腰三角形三线合一、四边形内角和性质,难度中等.利用角平分线的性质巧妙地构造出全等三角形是关键.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案
相关题目
19.下列实数:-$\frac{π}{4}$,0,$\sqrt{27}$,-$\frac{22}{7}$,$\root{3}{-\frac{1}{8}}$,-0.020020002…(每两个2之间依次增加一个0),其中是无理数的有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
6.将△ABC绕O点顺时针旋转50°得△A1B1C1(A、B分别对应A1、B1),则直线AB与直线A1B1的夹角(锐角)为( )
| A. | 130° | B. | 50° | C. | 40° | D. | 60° |
3. 如图,在△ABC中,已知点D,E,F分别为边BC,AD,CE的中点,且S△ABC=8cm2,则S阴影等于( )
如图,在△ABC中,已知点D,E,F分别为边BC,AD,CE的中点,且S△ABC=8cm2,则S阴影等于( )
 如图,在△ABC中,已知点D,E,F分别为边BC,AD,CE的中点,且S△ABC=8cm2,则S阴影等于( )
如图,在△ABC中,已知点D,E,F分别为边BC,AD,CE的中点,且S△ABC=8cm2,则S阴影等于( )| A. | 4cm2 | B. | 2cm2 | C. | 1cm2 | D. | 6cm2 |
20.针对关于x的分式方程$\frac{m}{x+6}$=1.下列说法正确的是( )
| A. | 方程的解是x=m-6 | B. | m>6时,方程的解是正数 | ||
| C. | m<6时,方程的解为负数 | D. | 无法确定 |
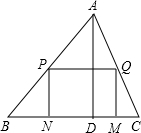 一块材料的形状是锐角三角形ABC,边BC=12cm,高AD=8cm,把它加工成矩形零件如图,要使矩形的一边在BC上,其余两个顶点分别在AB,AC上.且矩形的长与宽的比为3:2,求这个矩形零件的边长.
一块材料的形状是锐角三角形ABC,边BC=12cm,高AD=8cm,把它加工成矩形零件如图,要使矩形的一边在BC上,其余两个顶点分别在AB,AC上.且矩形的长与宽的比为3:2,求这个矩形零件的边长.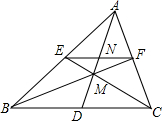 如图,E、F分别在△ABC的边AC、AB上,EF∥BC,BE与CF相交于M,AM交BC于D,交EF于N,求证:BD=DC.
如图,E、F分别在△ABC的边AC、AB上,EF∥BC,BE与CF相交于M,AM交BC于D,交EF于N,求证:BD=DC.