题目内容
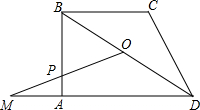 如图,梯形ABCD中,AD∥BC,∠A=90°,BC=CD,点O是对角线BD的中点,BD=5,tan∠DBC=
如图,梯形ABCD中,AD∥BC,∠A=90°,BC=CD,点O是对角线BD的中点,BD=5,tan∠DBC=| 4 |
| 3 |
(1)求梯形ABCD的周长;
(2)当△APM和△ABD相似时,求BP的值.
考点:相似三角形的判定与性质,梯形
专题:
分析:(1)由tan∠DBC=
,且AD∥BC可求得AB=4,AD=3,再过点C作CE⊥AD交AD于点E,在Rt△CED中可求得CD的长,可求得其周长;
(2)由△APM和△ABD相似可知∠M=∠B,可得∠BPO=∠ODA,可证得△BOP∽△BAD,利用相似比可求得BP.
| 4 |
| 3 |
(2)由△APM和△ABD相似可知∠M=∠B,可得∠BPO=∠ODA,可证得△BOP∽△BAD,利用相似比可求得BP.
解答:解:(1)∵AD∥BC,
∴∠BDA=∠DBC,
∴tan∠BDA=∠DBC=
,
∴
=
,且BD=5,
∴AB=4,AD=3,
如图,过点C作CE⊥AD交AD于点E,
则CE=AB=4,
设BC=CD=x,则DE=3-x,
在Rt△CED中,由勾股定理可得:x2=42+(3-x)2,解得x=
,
∴AB+BC+CD+DA=4+3+
+
=
,
即梯形ABCD的周长为
;
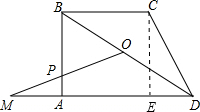
(2)当△APM和△ABD相似时
有∠PMA=∠BDA或∠PMA=∠ABD,
当∠PMA=∠BDA时,则OM=OD,且O为BD中点,所以OM=OD=OA,此时M点与A点重合,不符合题意,
当∠PMA=∠ABD时,
∵∠PMA+∠MPA=∠PMA+∠BPO=90°,∠PBO+∠BDA=90°,
∴∠BPO=∠BDA,且∠ABD为公共角,
∴△BPO∽△BDA,
∴
=
,即
=
,
解得BP=
.
∴∠BDA=∠DBC,
∴tan∠BDA=∠DBC=
| 4 |
| 3 |
∴
| AB |
| AD |
| 4 |
| 3 |
∴AB=4,AD=3,
如图,过点C作CE⊥AD交AD于点E,
则CE=AB=4,
设BC=CD=x,则DE=3-x,
在Rt△CED中,由勾股定理可得:x2=42+(3-x)2,解得x=
| 25 |
| 6 |
∴AB+BC+CD+DA=4+3+
| 25 |
| 6 |
| 25 |
| 6 |
| 46 |
| 3 |
即梯形ABCD的周长为
| 46 |
| 3 |

(2)当△APM和△ABD相似时
有∠PMA=∠BDA或∠PMA=∠ABD,
当∠PMA=∠BDA时,则OM=OD,且O为BD中点,所以OM=OD=OA,此时M点与A点重合,不符合题意,
当∠PMA=∠ABD时,
∵∠PMA+∠MPA=∠PMA+∠BPO=90°,∠PBO+∠BDA=90°,
∴∠BPO=∠BDA,且∠ABD为公共角,
∴△BPO∽△BDA,
∴
| BP |
| BD |
| BO |
| BA |
| BP |
| 5 |
| ||
| 4 |
解得BP=
| 25 |
| 8 |
点评:本题主要考查相似三角形的判定和性质,在(1)中求得BC长是解题的关键,在(2)中证明△BPO∽△BDA是解题的关键.

练习册系列答案
 学习实践园地系列答案
学习实践园地系列答案
相关题目
符号“f”表示一种运算,它对一些数的运算结果如下:
(1)f(1)=0,f(2)=1,f(3)=2,f(4)=3,…
(2)f(
)=2,f(
)=3,f(
)=4,f(
)=5,…
利用以上规律计算f(
)-f(2015)结果是( )
(1)f(1)=0,f(2)=1,f(3)=2,f(4)=3,…
(2)f(
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 5 |
利用以上规律计算f(
| 1 |
| 2014 |
| A、-1 | B、0 | C、1 | D、不能确定 |
 a,b两数在数轴上的位置如图所示,下列结论中正确的是( )
a,b两数在数轴上的位置如图所示,下列结论中正确的是( )| A、a<0,b>0 |
| B、a+b<0 |
| C、ab>0 |
| D、a-b<0 |
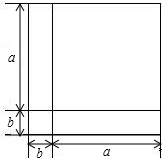 如图,大正方形是由两个小正方形和两个长方形拼成的.
如图,大正方形是由两个小正方形和两个长方形拼成的.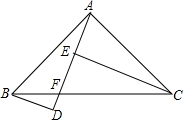 如图,△ABC中,∠BAC=90°,AB=AC,F是BC上一点,BD⊥AF交AF的延长线于D,CE⊥AF于E,已知CE=5,BD=2,则ED=
如图,△ABC中,∠BAC=90°,AB=AC,F是BC上一点,BD⊥AF交AF的延长线于D,CE⊥AF于E,已知CE=5,BD=2,则ED=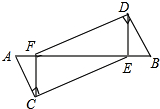 如图,已知A,F,E,B四点共线,AC⊥CE,BD⊥DF,AE=BF,AC=BD.
如图,已知A,F,E,B四点共线,AC⊥CE,BD⊥DF,AE=BF,AC=BD.