题目内容
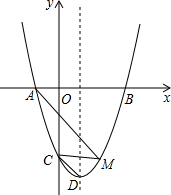 抛物线y=x2+bx+c与x轴交于A(-1,0)、B两点,与y轴交于C(0,-3),顶点为D,点M是抛物线上任意一点.
抛物线y=x2+bx+c与x轴交于A(-1,0)、B两点,与y轴交于C(0,-3),顶点为D,点M是抛物线上任意一点.(1)求抛物线解析式;
(2)在抛物线对称轴右侧的图象上是否存在点M,使∠AMC=∠MCD?若存在,求出点M的坐标;若不存在,请说明理由;
(3)点N为抛物线对称轴上一动点,若以B、N、C为顶点的三角形为直角三角形,求出所有相应的点N的坐标.
考点:二次函数综合题
专题:
分析:(1)直接利用待定系数法求出抛物线解析式进而得出答案即可;
(2)首先求出lCD:y=-x-3,lAM:y=-x-1进而得出,当y=x2-2x-3=-x-1时,AM∥CD,求出M点坐标即可;
(3)①若∠BNC=90°,则BC2=BN2+NC2,②若∠NBC=90°,则NC2=BN2+BC2,③若∠NCB=90°,则BN2=NC2+BC2,分别求出N点坐标即可.
(2)首先求出lCD:y=-x-3,lAM:y=-x-1进而得出,当y=x2-2x-3=-x-1时,AM∥CD,求出M点坐标即可;
(3)①若∠BNC=90°,则BC2=BN2+NC2,②若∠NBC=90°,则NC2=BN2+BC2,③若∠NCB=90°,则BN2=NC2+BC2,分别求出N点坐标即可.
解答: 解:(1)抛物线y=x2+bx+c过(-1,0)(0,-3)
解:(1)抛物线y=x2+bx+c过(-1,0)(0,-3)
∴
解得:
∴抛物线解析式为:y=x2-2x-3;
(2)存在.
如图1,当AM∥CD时,∠AMC=∠MCD,
由(1)可得抛物线y=x2-2x-3=(x-1)2-4
∴D(1,-4)
设直线CD为:y=kx-3过D(1,-4)
∴lCD:y=-x-3
设直线AM为:y=-x+b过A(-1,0)
∴lAM:y=-x-1
当y=x2-2x-3=-x-1时,AM∥CD,
∴x1=-1(舍),x2=2,
∴y=22-2×2-3=-3,
∴M(2,-3);
(3)设N(1,n),则BN=
,NC=
,BC=3
,
①如图2,若∠BNC=90°,则BC2=BN2+NC2,即18=4+n2+1+9+6n+n2
∴n2+3n-2=0,
∴解得:n=
∴N(1,
)或N(1,
),
②若∠NBC=90°,则NC2=BN2+BC2,即1+9+6n+n2=4+n2+18
∴6n=12,
∴n=2
∴N(1,2),
③若∠NCB=90°,则BN2=NC2+BC2,即1+9+6n+n2+18=4+n2
∴6n=-24,
∴n=-4
∴N(1,-4),
综上,当N(1,
)或N(1,
)或N(1,2)或N(1,-4)时,以B、N、C为顶点的三角形为直角三角形.
 解:(1)抛物线y=x2+bx+c过(-1,0)(0,-3)
解:(1)抛物线y=x2+bx+c过(-1,0)(0,-3)∴
|
解得:
|
∴抛物线解析式为:y=x2-2x-3;
(2)存在.
如图1,当AM∥CD时,∠AMC=∠MCD,
由(1)可得抛物线y=x2-2x-3=(x-1)2-4
∴D(1,-4)
设直线CD为:y=kx-3过D(1,-4)
∴lCD:y=-x-3
设直线AM为:y=-x+b过A(-1,0)
∴lAM:y=-x-1
当y=x2-2x-3=-x-1时,AM∥CD,
∴x1=-1(舍),x2=2,
∴y=22-2×2-3=-3,
∴M(2,-3);
(3)设N(1,n),则BN=
| 4+n2 |
| 1+(-3-n)2 |
| 2 |
①如图2,若∠BNC=90°,则BC2=BN2+NC2,即18=4+n2+1+9+6n+n2

∴n2+3n-2=0,
∴解得:n=
-3±
| ||
| 2 |
∴N(1,
-3+
| ||
| 2 |
-3-
| ||
| 2 |
②若∠NBC=90°,则NC2=BN2+BC2,即1+9+6n+n2=4+n2+18
∴6n=12,
∴n=2
∴N(1,2),
③若∠NCB=90°,则BN2=NC2+BC2,即1+9+6n+n2+18=4+n2
∴6n=-24,
∴n=-4
∴N(1,-4),
综上,当N(1,
-3+
| ||
| 2 |
-3-
| ||
| 2 |
点评:此题主要考查了二次函数综合以及勾股定理的应用和待定系数法求函数解析式等知识,利用分类讨论得出N点坐标是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,在正方形网格中有一等腰△ABC,AB=AC=5,BC=6,请用两种方法画一条直线将△ABC的面积与周长同时平分,要求:
如图,在正方形网格中有一等腰△ABC,AB=AC=5,BC=6,请用两种方法画一条直线将△ABC的面积与周长同时平分,要求: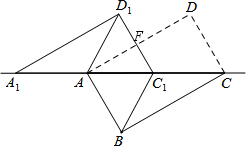 如图,将矩形ABCD沿对角线AC剪开,再把△ACD沿CA方向平移得到△A1C1D1,连结AD1、BC1.若∠ACB=30°,AB=2,CC1=x,四边形ABC1D1的面积为S.
如图,将矩形ABCD沿对角线AC剪开,再把△ACD沿CA方向平移得到△A1C1D1,连结AD1、BC1.若∠ACB=30°,AB=2,CC1=x,四边形ABC1D1的面积为S.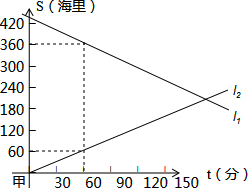 A、B两船同时从相距450海里的甲、乙两港相向而行,s(海里)表示轮船与甲港的距离,t(分钟)表示轮船行驶的时间,如图所示,l1、l2分别表示两船的s与t的关系.
A、B两船同时从相距450海里的甲、乙两港相向而行,s(海里)表示轮船与甲港的距离,t(分钟)表示轮船行驶的时间,如图所示,l1、l2分别表示两船的s与t的关系. 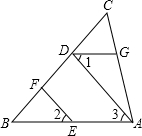 如图,EF∥AD,∠1=∠2,∠BAC=75°.求∠AGD的度数.
如图,EF∥AD,∠1=∠2,∠BAC=75°.求∠AGD的度数. 如图,在△BOD中,OB=7,OD=3,将△BOD绕点O逆时针旋转90°至△AOC的位置,求图中阴影部分的面积.
如图,在△BOD中,OB=7,OD=3,将△BOD绕点O逆时针旋转90°至△AOC的位置,求图中阴影部分的面积.