题目内容
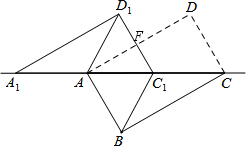 如图,将矩形ABCD沿对角线AC剪开,再把△ACD沿CA方向平移得到△A1C1D1,连结AD1、BC1.若∠ACB=30°,AB=2,CC1=x,四边形ABC1D1的面积为S.
如图,将矩形ABCD沿对角线AC剪开,再把△ACD沿CA方向平移得到△A1C1D1,连结AD1、BC1.若∠ACB=30°,AB=2,CC1=x,四边形ABC1D1的面积为S.(1)线段AD1的长度最小值是
(2)当x为何时,四边形ABC1D1是菱形?并说明理由;
(3)求S与x的函数关系式,并在直角坐标系中画出这个函数的图象.
考点:矩形的性质,菱形的判定,平移的性质
专题:
分析:(1)当AD1⊥AC时,线段AD1的长度最小,再根据解直角三角形求解.
(2)四边形ABC1D1是菱形,可以得出△AD1C1是等边三角形,进而求出x的值.
(3)作C1E⊥AB于点E,求出EC1用平行四边形的面积公式求出关于S与x的函数关系式,注意函数关系式分两种情况并画出图象.
(2)四边形ABC1D1是菱形,可以得出△AD1C1是等边三角形,进而求出x的值.
(3)作C1E⊥AB于点E,求出EC1用平行四边形的面积公式求出关于S与x的函数关系式,注意函数关系式分两种情况并画出图象.
解答:解:(1)当AD1⊥AC时,线段AD1的长度最小;
∵矩形ABCD中,∠ACB=30°,AB=2,
∴∠D1A1C1=∠DAC=∠ACB=30°,C1D1=CD=AB=2,∠A1D1C1=∠D=90°,
∴∠A1C1D1=60°,
∴AC1=C1D1•cos60°=2×
=1,AD1=C1D1•sin60°=2×
=
,
∵AC=2CD=4,
∴x=AC-AC1=4-1=3;
故答案为:
,3.
(2)当x=2时,四边形ABC1D1是菱形.
理由:四边形ABC1D1是菱形
∴C1D1=AD1
∵∠A1C1D1=60°,C1D1=2,
∴△AD1C1是等边三角形,
∴AD1=AC1=C1D1=2
x=AB-AC1=4-2=2
∴当x=2时,四边形ABC1D1是菱形;
(3)
①当0<x<4时,如图作C1E⊥AB于点E
∵∠ACB=30°,AB=2
∴AC=4,AC1=4-x
∵C1E∥BC
∴∠AC1E=∠ACB=30°
∴AE=
,EC1=
(4-x)
∴S=AB×EC1=2×
(4-x)=4
-
x
S=-
x+4
②当x>4时,如图2,作C1E⊥AB于点E

∵∠ACB=30°,AB=2
∴AC=4,AC1 =x-4
∵C1E∥BC
∴∠AC1E=∠ACB=30°
∴AE=
(x-4),EC1=
(x-4)
∴S=AB×EC1=2×
(x-4)=
x-4
图象:

∵矩形ABCD中,∠ACB=30°,AB=2,
∴∠D1A1C1=∠DAC=∠ACB=30°,C1D1=CD=AB=2,∠A1D1C1=∠D=90°,
∴∠A1C1D1=60°,
∴AC1=C1D1•cos60°=2×
| 1 |
| 2 |
| ||
| 2 |
| 3 |
∵AC=2CD=4,
∴x=AC-AC1=4-1=3;
故答案为:
| 3 |
(2)当x=2时,四边形ABC1D1是菱形.
理由:四边形ABC1D1是菱形
∴C1D1=AD1
∵∠A1C1D1=60°,C1D1=2,
∴△AD1C1是等边三角形,
∴AD1=AC1=C1D1=2
x=AB-AC1=4-2=2
∴当x=2时,四边形ABC1D1是菱形;
(3)

①当0<x<4时,如图作C1E⊥AB于点E
∵∠ACB=30°,AB=2
∴AC=4,AC1=4-x
∵C1E∥BC
∴∠AC1E=∠ACB=30°
∴AE=
| 4-x |
| 2 |
| ||
| 2 |
∴S=AB×EC1=2×
| ||
| 2 |
| 3 |
| 3 |
S=-
| 3 |
| 3 |
②当x>4时,如图2,作C1E⊥AB于点E

∵∠ACB=30°,AB=2
∴AC=4,AC1 =x-4
∵C1E∥BC
∴∠AC1E=∠ACB=30°
∴AE=
| 1 |
| 2 |
| ||
| 2 |
∴S=AB×EC1=2×
| ||
| 2 |
| 3 |
| 3 |
图象:

点评:本题主要考查矩形的性质、等边三角形的判定及解直角三角形的知识.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
下列选项中,可以用来说明命题“两个锐角的和是钝角”是假命题的是( )
| A、∠A=30°,∠B=50° |
| B、∠A=30°,∠B=70° |
| C、∠A=30°,∠B=90° |
| D、∠A=30°,∠B=110° |
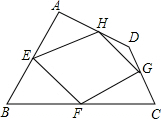 已知:如图,四边形ABCD四条边上的中点分别为E、F、G、H,顺次连接EF、FG、GH、HE,得到四边形EFGH(即四边形ABCD的中点四边形).
已知:如图,四边形ABCD四条边上的中点分别为E、F、G、H,顺次连接EF、FG、GH、HE,得到四边形EFGH(即四边形ABCD的中点四边形).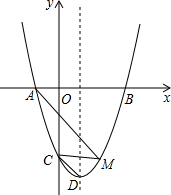 抛物线y=x2+bx+c与x轴交于A(-1,0)、B两点,与y轴交于C(0,-3),顶点为D,点M是抛物线上任意一点.
抛物线y=x2+bx+c与x轴交于A(-1,0)、B两点,与y轴交于C(0,-3),顶点为D,点M是抛物线上任意一点.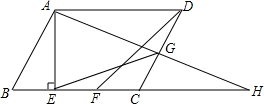 已知在平行四边形ABCD中,AE⊥BC,垂足为E,CE=CD,F为CE的中点,G为CD上的一点,连接DF、EG、AG,并延长AG、BC交于点H,∠DFC=∠EGC.
已知在平行四边形ABCD中,AE⊥BC,垂足为E,CE=CD,F为CE的中点,G为CD上的一点,连接DF、EG、AG,并延长AG、BC交于点H,∠DFC=∠EGC.