题目内容
9.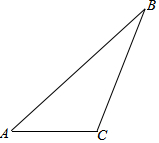 如图,在△ABC中,先按如下步骤尺规作图再计算:
如图,在△ABC中,先按如下步骤尺规作图再计算:(1)作AD平分∠BAC,交BC于D;
(2)作AD的垂直平分线MN分别交AB、AC于点E、F;
(3)连接DE、DF.若BD=6,AF=4,CD=3,求BE的长.
分析 (1)∠BAC的平分线AD如图所示.
(2)线段AD的垂直平分线MN,分别交AB、AC于点E、F,如图所示.
(3)首先证明四边形AEDF是菱形,推出AE=DE=AF=DF=4,由DE∥AC,推出$\frac{BE}{EA}$=$\frac{BD}{DC}$,由此即可解决问题.
解答 解:(1)∠BAC的平分线AD如图所示.
(2)线段AD的垂直平分线MN,分别交AB、AC于点E、F,如图所示.
(3)∵EA=ED,FA=FD,
∴∠EAD=∠EDA,∠FAD=∠FDA,
∵∠EAD=∠FAD,
∴∠EDA=∠FAD,∠EAD=∠FDA,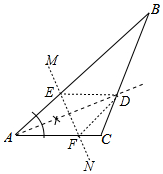
∴DE∥AF,AE∥DF,
∴四边形AEDF是平行四边形,∵EA=ED,
∴四边形AEDF是菱形,
∴AE=DE=AF=DF=4,
∵DE∥AC,
∴$\frac{BE}{EA}$=$\frac{BD}{DC}$,
∴$\frac{BE}{4}$=$\frac{6}{3}$,
∴BE=8.
点评 本题考查复杂作图、线段的垂直平分线的性质、菱形的判定和性质、平行线分线段成比例定理等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.

练习册系列答案
相关题目
19.若a+b<0,$\frac{b}{a}$>0,则下列成立的是( )
| A. | a>0,b>0 | B. | a>0,b<0 | C. | a<0,b<0 | D. | a<0,b>0 |
1.-$\frac{1}{4}$的相反数是( )
| A. | 4 | B. | -$\frac{1}{4}$ | C. | $\frac{1}{4}$ | D. | -4 |
18.在实数0,(-$\sqrt{3}$)0,(-$\frac{2}{3}$)-2,|-2|中,最大的是( )
| A. | 0 | B. | (-$\sqrt{3}$)0 | C. | (-$\frac{2}{3}$)-2 | D. | |-2| |
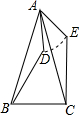 如图,在△ABC中,∠BAC=45°,AB=AC,D为△ABC内一点,AD=4,如果把△ABD绕点A按逆时针方向旋转,使AB与AC重合,求点D运动的路径长.
如图,在△ABC中,∠BAC=45°,AB=AC,D为△ABC内一点,AD=4,如果把△ABD绕点A按逆时针方向旋转,使AB与AC重合,求点D运动的路径长. 如图AB∥CD,BC∥DE,∠B=120°,则∠D的度数是60°.
如图AB∥CD,BC∥DE,∠B=120°,则∠D的度数是60°. 如图,△ABC中,DE∥BC,则$\frac{AB}{()}$=$\frac{()}{()}$.
如图,△ABC中,DE∥BC,则$\frac{AB}{()}$=$\frac{()}{()}$.