题目内容
9.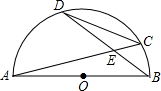 半圆O的直径AB=9,两弦AB、CD相交于点E,弦CD=$\frac{27}{5}$,且BD=7,则DE=3$\sqrt{2}$.
半圆O的直径AB=9,两弦AB、CD相交于点E,弦CD=$\frac{27}{5}$,且BD=7,则DE=3$\sqrt{2}$.
分析 根据圆周角定理得出的两组相等的对应角,易证得△AEB∽△DEC,根据CD、AB的长,即可求出两个三角形的相似比;设BE=x,则DE=7-x,然后根据相似比表示出AE、EC的长,连接BC,首先在Rt△BEC中,根据勾股定理求得BC的表达式,然后在Rt△ABC中,由勾股定理求得x的值,进而可求出DE的长.
解答 解:∵∠D=∠A,∠DCA=∠ABD,
∴△AEB∽△DEC,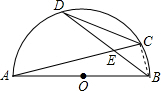
∴$\frac{EC}{BE}$=$\frac{DE}{AE}$=$\frac{DC}{AB}$=$\frac{3}{5}$,
设BE=x,则DE=7-x,EC=$\frac{3}{5}$x,AE=$\frac{5}{3}$(7-x),
连接BC,则∠ACB=90°,
Rt△BCE中,BE=x,EC=$\frac{3}{5}$x,则BC=$\frac{4}{5}$x,
在Rt△ABC中,AC=AE+EC=$\frac{35}{3}$-$\frac{16}{15}$x,BC=$\frac{4}{5}$x,
由勾股定理,得:AB2=AC2+BC2,
即:92=($\frac{35}{3}$-$\frac{16}{15}$x)2+($\frac{4}{5}$x)2,
整理,得x2-14x+31=0,
解得:x1=7+3$\sqrt{2}$(不合题意舍去),x2=7-3$\sqrt{2}$,
则DE=7-x=3$\sqrt{2}$.
故答案为:3$\sqrt{2}$
点评 此题主要考查了圆周角定理、相似三角形的判定和性质、勾股定理的应用等知识;本题要特别注意的是BE、DE不是相似三角形的对应边,它们的比不等于相似比,以免造成错解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
18.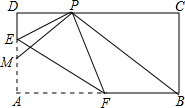 如图,已知在矩形ABCD中,AB=4,BC=2,点M,E在AD上,点F在边AB上,并且DM=1,现将△AEF沿着直线EF折叠,使点A落在边CD上的点P处,则当PB+PM的和最小时,ME的长度为( )
如图,已知在矩形ABCD中,AB=4,BC=2,点M,E在AD上,点F在边AB上,并且DM=1,现将△AEF沿着直线EF折叠,使点A落在边CD上的点P处,则当PB+PM的和最小时,ME的长度为( )
 如图,已知在矩形ABCD中,AB=4,BC=2,点M,E在AD上,点F在边AB上,并且DM=1,现将△AEF沿着直线EF折叠,使点A落在边CD上的点P处,则当PB+PM的和最小时,ME的长度为( )
如图,已知在矩形ABCD中,AB=4,BC=2,点M,E在AD上,点F在边AB上,并且DM=1,现将△AEF沿着直线EF折叠,使点A落在边CD上的点P处,则当PB+PM的和最小时,ME的长度为( )| A. | $\frac{1}{3}$ | B. | $\frac{4}{9}$ | C. | $\frac{2}{3}$ | D. | $\frac{5}{9}$ |
 如图,P是⊙O直径CB延长线上一点,A是⊙O上一点,PA=3,PB=1,BC=8
如图,P是⊙O直径CB延长线上一点,A是⊙O上一点,PA=3,PB=1,BC=8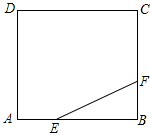 如图,正方形ABCD的边长为3,点E,F分别在边AB,BC上,AE=BF=1,小球P从点E出发沿直线向点F运动,每当碰到正方形的边时反弹,反弹时反射角等于入射角.当小球P第一次碰到BC边时,小球P所经过的路程为$\sqrt{5}$;当小球P第一次碰到AD边时,小球P所经过的路程为$\frac{5}{2}\sqrt{5}$;当小球P第n(n为正整数)次碰到点F时,小球P所经过的路程为$6\sqrt{5}n\;-5\sqrt{5}$.
如图,正方形ABCD的边长为3,点E,F分别在边AB,BC上,AE=BF=1,小球P从点E出发沿直线向点F运动,每当碰到正方形的边时反弹,反弹时反射角等于入射角.当小球P第一次碰到BC边时,小球P所经过的路程为$\sqrt{5}$;当小球P第一次碰到AD边时,小球P所经过的路程为$\frac{5}{2}\sqrt{5}$;当小球P第n(n为正整数)次碰到点F时,小球P所经过的路程为$6\sqrt{5}n\;-5\sqrt{5}$.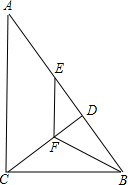 如图,在Rt△ABC中,∠ACB=90°,CD是斜边AB上的高,点E在边AB上,且BE=BC,过点E作EF∥AC,交CD于F点,连接BF.
如图,在Rt△ABC中,∠ACB=90°,CD是斜边AB上的高,点E在边AB上,且BE=BC,过点E作EF∥AC,交CD于F点,连接BF.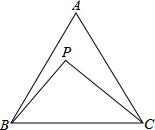 如图,等边三角形ABC中,点P在△ABC内部,且∠BPC=90°.若AB=7,CP=2$\sqrt{7}$,则tan∠ACP=$\frac{24-7\sqrt{3}}{49}$.
如图,等边三角形ABC中,点P在△ABC内部,且∠BPC=90°.若AB=7,CP=2$\sqrt{7}$,则tan∠ACP=$\frac{24-7\sqrt{3}}{49}$.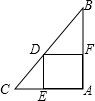 如图,正方形DEAF内接于△ABC,已知AC=8,AB=16,那么正方形的边长是$\frac{16}{3}$.
如图,正方形DEAF内接于△ABC,已知AC=8,AB=16,那么正方形的边长是$\frac{16}{3}$.