Question

20．如图，在平面直角坐标系中，点O为坐标原点，△ABC是边长为16的正三角形，点A、B分别在x轴的正半轴、y轴的正半轴上滑动，点C在第一象限，连接OC，则线段OC的长的最大值是8+8$\sqrt{3}$．

Answer 1

分析 取AB的中点D，连接OD、CD，根据直角三角形斜边上的中线以及等边三角形的性质，即可得出OD、CD的长度，再根据三角形的三边关系即可得出OC＜OD+CD，由此即可得出当点O、C、D三点共线时，OC=OD=CD的值最大，代入数据即可得出结论．

解答 解：取AB的中点D，连接OD、CD，如图所示．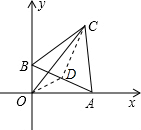
∵△AOB为直角三角形，D为AB的中点，
∴OD=$\frac{1}{2}$AB=8，
∵△ABC是边长为16的正三角形，D为AB的中点，
∴CD=$\frac{\sqrt{3}}{2}$AB=8$\sqrt{3}$．
在△OCD中，OC＜OD+CD．
当点O、C、D三点共线时，OC=OD+CD最大，
此时OC=8+8$\sqrt{3}$．
故答案为：8+8$\sqrt{3}$．

点评 本题考查了直角三角形斜边上的中线、等边三角形的性质以及三角形的三边关系，解题的关键是找出当点O、C、D三点共线时OC的长取最大值．本题属于基础题，难度不大，解决该题型题目时，利用数形结合解决问题是关键．