题目内容
4.等边三角形的高为2,则它的面积是$\frac{4\sqrt{3}}{3}$.分析 由等边三角形的高可将其边长求出,然后代入三角形面积公式可将其面积求出.
解答 解:设等边三角形的边长为a,高为h,则:($\frac{1}{2}$a)2+h2=a2,即($\frac{1}{2}$a)2+22=a2
可得:a=$\frac{4\sqrt{3}}{3}$
∴S=$\frac{1}{2}$ah=$\frac{1}{2}$×$\frac{4\sqrt{3}}{3}$×2=$\frac{4\sqrt{3}}{3}$.
故答案为:$\frac{4\sqrt{3}}{3}$.
点评 本题主要考查等边三角形的性质,三角形的面积的求法,熟练掌握等边三角形的性质是解题的关键.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
14. 如图,下列说法正确的是( )
如图,下列说法正确的是( )
 如图,下列说法正确的是( )
如图,下列说法正确的是( )| A. | ∠1和∠B是同旁内角 | B. | ∠1和∠C是内错角 | ||
| C. | ∠2和∠B是同位角 | D. | ∠3和∠C同旁内角 |
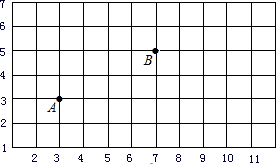 如图,点A用(3,3)表示,点B用(7,5)表示,若用(3,3)→(5,3)→(5,4)→(7,4)→(7,5)表示由A到B的一种走法,并规定从A到B只能向上或向右走,用上述表示法写出另两种走法,并判断这几种走法的路程是否相等.
如图,点A用(3,3)表示,点B用(7,5)表示,若用(3,3)→(5,3)→(5,4)→(7,4)→(7,5)表示由A到B的一种走法,并规定从A到B只能向上或向右走,用上述表示法写出另两种走法,并判断这几种走法的路程是否相等.