题目内容
16．若反比例函数y=$\frac{k+1}{x}$的图象在其每个象限内，y随着x的增大而增大，则k的值可以为（ ）| A． | 0 | B． | 1 | C． | -2 | D． | 3 |
分析 先根据反比例函数的性质得出k+1＜0，再解不等式求出k的取值范围．
解答 解：∵反比例函数的图象在其每个象限内，y随着x的增大而增大，
∴k+1＜0，
∴k＜-1，只有-2合适．
故选C．
点评 本题考查了反比例函数的图象和性质：①、当k＞0时，图象分别位于第一、三象限；当k＜0时，图象分别位于第二、四象限．②、当k＞0时，在同一个象限内，y随x的增大而减小；当k＜0时，在同一个象限，y随x的增大而增大．
练习册系列答案
相关题目
6．计算：2-$\sqrt{9}$=（ ）
| A． | -1 | B． | -3 | C． | 3 | D． | 5 |
1．
如图，将图中的福娃“欢欢”通过平移可得到下列图为（ ）
如图，将图中的福娃“欢欢”通过平移可得到下列图为（ ）| A． |  | B． |  | C． |  | D． |  |
8．无论x取什么数时，总有意义的分式是（ ）
| A． | $\frac{2x}{{{x^2}+0.2}}$ | B． | $\frac{x}{2x+1}$ | C． | $\frac{3x}{{{x^3}+1}}$ | D． | $\frac{x-5}{x^2}$ |
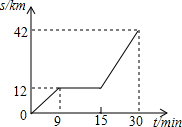如图是某汽车行驶的路S（km）与时间t（min）的函数关系图，观察图中所提供的信息，解答下列问题：