题目内容
10.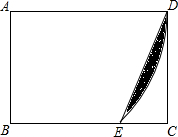 如图,在矩形ABCD中,AB=$\sqrt{2}$,BC=2,以A为圆心,AD为半径画弧交线段BC与E,连接DE,则图中阴影部分的面积为$\frac{π}{2}$-$\sqrt{2}$.(结果保留π)
如图,在矩形ABCD中,AB=$\sqrt{2}$,BC=2,以A为圆心,AD为半径画弧交线段BC与E,连接DE,则图中阴影部分的面积为$\frac{π}{2}$-$\sqrt{2}$.(结果保留π)
分析 如图,连接AE,作EM⊥AD于M,则四边形ABEM是矩形.利用勾股定理求出BE,即可发现四边形ABEM是正方形,由此即可解决问题.
解答 解:如图,连接AE,作EM⊥AD于M,则四边形ABEM是矩形.
在Rt△ABE中,∵AE=AD=2.AB=$\sqrt{2}$,
∴BE=$\sqrt{A{E}^{2}-A{B}^{2}}$=$\sqrt{2}$,
∴AB=BE,
∴四边形ABEM是正方形,
∴∠EAM=45°,EM=AB=$\sqrt{2}$,
∴S阴=S扇形ADE-S△ADE=$\frac{45•π•{2}^{2}}{360}$-$\frac{1}{2}$•2•$\sqrt{2}$=$\frac{π}{2}$-$\sqrt{2}$,
故答案为$\frac{π}{2}$-$\sqrt{2}$.
点评 本题考查矩形的性质和判定、正方形的性质和判定、扇形的面积公式.勾股定理等知识,解题的关键是学会利用分割法求阴影部分面积,属于中考常考题型.

练习册系列答案
相关题目
1.下列运算中,结果正确的是( )
| A. | -1-1=0 | B. | -$\frac{3}{7}$+$\frac{6}{7}$=-$\frac{9}{7}$ | C. | $\frac{1}{4}$-$\frac{3}{4}$=-$\frac{1}{2}$ | D. | -5-(-2)+(-3)=-10 |
5.下列图形中,是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
15.某校在“6•26国际禁毒日”前组织七年级全体学生320人进行了一次“毒品预防知识”竞赛,赛后随机抽取了部分学生成绩进行统计,制作如表频数分布表和频数分布直方图,请根据图表提供的信息,解答下列问题:

(1)表中a=8,b=0.3,并补全直方图
(2)若用扇形统计图描述此成绩分布情况,则分数段80≤x<100对应扇形的圆心角度数是144°;
(3)请估计该年级分数在60≤x<100的学生有多少人?
| 少分数段(x表示分数) | 频数 | 频率 |
| 50≤x<60 | 4 | 0.1 |
| 60≤x<70 | a | 0.2 |
| 70≤x<80 | 12 | b |
| 80≤x<90 | 10 | 0.25 |
| 90≤x<100 | 6 | 0.15 |

(1)表中a=8,b=0.3,并补全直方图
(2)若用扇形统计图描述此成绩分布情况,则分数段80≤x<100对应扇形的圆心角度数是144°;
(3)请估计该年级分数在60≤x<100的学生有多少人?
19.已知数据1、5、4、3、3、2,则下列关于这组数据的说法错误的是( )
| A. | 平均数和众数都是3 | B. | 中位数为3 | ||
| C. | 方差为10 | D. | 标准差是$\frac{{\sqrt{15}}}{3}$ |
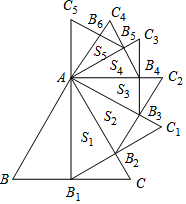 如图,正△ABC的边长为2,以BC边上的高AB1为边作正△AB1C1,△ABC与△AB1C1公共部分的面积记为S1;再以证△AB1C1,△ABC与△AB1C1公共部分的面积记为S1;再以正△AB1C1边B1C1上的高AB2为边作正△AB2C2,△AB1C1与△AB2C2公共部分的面积记为S2…,以此类推,则Sn=$\frac{\sqrt{3}}{2}$($\frac{3}{4}$)n.(用含n的式子表示)
如图,正△ABC的边长为2,以BC边上的高AB1为边作正△AB1C1,△ABC与△AB1C1公共部分的面积记为S1;再以证△AB1C1,△ABC与△AB1C1公共部分的面积记为S1;再以正△AB1C1边B1C1上的高AB2为边作正△AB2C2,△AB1C1与△AB2C2公共部分的面积记为S2…,以此类推,则Sn=$\frac{\sqrt{3}}{2}$($\frac{3}{4}$)n.(用含n的式子表示)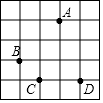 如图,每个小正方形的边长都是1,图中A,B,C,D四个点分别为小正方形的顶点,下列说法:
如图,每个小正方形的边长都是1,图中A,B,C,D四个点分别为小正方形的顶点,下列说法: