题目内容
2.有4张全新的扑克牌,其中黑桃、红桃各2张,它们的背面都一样,将它们洗匀后,背面朝上放到桌面上,从中任意摸出2张牌,摸出的花色不一样的概率是$\frac{2}{3}$.分析 利用列举法即可列举出所有各种灯可能的情况,然后利用概率公式即可求解.
解答 解:根据题意画图如下:
共有12中情况,从4张牌中任意摸出2张牌花色不一样的有8种可能,所以摸出花色不一样的概率是$\frac{8}{12}$=$\frac{2}{3}$;
故答案为:$\frac{2}{3}$.
点评 此题考查概率的求法:如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=$\frac{m}{n}$.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案
相关题目
12.稀土元素有独特的性能和广泛的应用,我国稀土资源的总储藏量为1050008000吨,是全世界稀土资源最丰富的国家,用科学记数法表示为( )
| A. | 1.05×1010吨 | B. | 1.05×109吨 | C. | 10.5×108吨 | D. | 1.105×1010吨 |
13.下列计算正确的是( )
| A. | xm+xm=x2m | B. | x3•x3=x6 | C. | 2-2=-4 | D. | x6÷x2=x3 |
17.下列命题中,错误的是( )
| A. | 矩形的对角线互相平分且相等 | |
| B. | 等腰三角形底边上的中点到两腰的距离相等 | |
| C. | 等腰梯形的两条对角线相等 | |
| D. | 对角线互相垂直的四边形是菱形 |
7.在一个不透明的口袋里装着只有颜色不同的黑、白两种颜色的球共50只,某学习小组做摸球实验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复以上步骤,下表为实验的一组统计数据:
请估算口袋中白球的个数约为( )
| 摸球的次数n | 1000 | 1500 | 2000 | 5000 | 8000 | 10000 |
| 摸到白球的次数m | 582 | 960 | 1161 | 2954 | 4842 | 6010 |
| 摸到白球的频率 | 0.582 | 0.64 | 0.5805 | 0.5908 | 0.6053 | 0.601 |
| A. | 20 | B. | 25 | C. | 30 | D. | 35 |
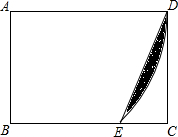 如图,在矩形ABCD中,AB=$\sqrt{2}$,BC=2,以A为圆心,AD为半径画弧交线段BC与E,连接DE,则图中阴影部分的面积为$\frac{π}{2}$-$\sqrt{2}$.(结果保留π)
如图,在矩形ABCD中,AB=$\sqrt{2}$,BC=2,以A为圆心,AD为半径画弧交线段BC与E,连接DE,则图中阴影部分的面积为$\frac{π}{2}$-$\sqrt{2}$.(结果保留π)