题目内容
20.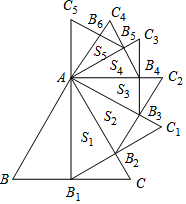 如图,正△ABC的边长为2,以BC边上的高AB1为边作正△AB1C1,△ABC与△AB1C1公共部分的面积记为S1;再以证△AB1C1,△ABC与△AB1C1公共部分的面积记为S1;再以正△AB1C1边B1C1上的高AB2为边作正△AB2C2,△AB1C1与△AB2C2公共部分的面积记为S2…,以此类推,则Sn=$\frac{\sqrt{3}}{2}$($\frac{3}{4}$)n.(用含n的式子表示)
如图,正△ABC的边长为2,以BC边上的高AB1为边作正△AB1C1,△ABC与△AB1C1公共部分的面积记为S1;再以证△AB1C1,△ABC与△AB1C1公共部分的面积记为S1;再以正△AB1C1边B1C1上的高AB2为边作正△AB2C2,△AB1C1与△AB2C2公共部分的面积记为S2…,以此类推,则Sn=$\frac{\sqrt{3}}{2}$($\frac{3}{4}$)n.(用含n的式子表示)
分析 由AB1为边长为2的等边三角形ABC的高,利用三线合一得到B1为BC的中点,求出BB1的长,利用勾股定理求出AB1的长,进而求出S1,同理求出S2,依此类推,得到Sn.
解答 解:∵等边三角形ABC的边长为2,AB1⊥BC,
∴BB1=1,AB=2,
根据勾股定理得:AB1=$\sqrt{3}$,
∴S1=$\frac{1}{2}$×$\frac{\sqrt{3}}{4}$×($\sqrt{3}$)2=$\frac{\sqrt{3}}{2}$($\frac{3}{4}$)1;
∵等边三角形AB1C1的边长为$\sqrt{3}$,AB2⊥B1C1,
∴B1B2=$\frac{\sqrt{3}}{2}$,AB1=$\sqrt{3}$,
根据勾股定理得:AB2=$\frac{3}{2}$,
∴S2=$\frac{1}{2}$×$\frac{\sqrt{3}}{4}$×($\frac{3}{2}$)2=$\frac{\sqrt{3}}{2}$($\frac{3}{4}$)2;
依此类推,Sn=$\frac{\sqrt{3}}{2}$($\frac{3}{4}$)n.
故答案为:$\frac{\sqrt{3}}{2}$($\frac{3}{4}$)n.
点评 此题考查了等边三角形的性质,属于规律型试题,熟练掌握等边三角形的性质是解本题的关键.

练习册系列答案
相关题目
15. 如图,∠BAC=90°,AD⊥BC,则图中互余的角有( )
如图,∠BAC=90°,AD⊥BC,则图中互余的角有( )
 如图,∠BAC=90°,AD⊥BC,则图中互余的角有( )
如图,∠BAC=90°,AD⊥BC,则图中互余的角有( )| A. | 2对 | B. | 3对 | C. | 4对 | D. | 5对 |
5.$\frac{1}{4}$的倒数是( )
| A. | 4 | B. | -4 | C. | $-\frac{1}{4}$ | D. | 0.4 |
12.稀土元素有独特的性能和广泛的应用,我国稀土资源的总储藏量为1050008000吨,是全世界稀土资源最丰富的国家,用科学记数法表示为( )
| A. | 1.05×1010吨 | B. | 1.05×109吨 | C. | 10.5×108吨 | D. | 1.105×1010吨 |
 如图,正方形ABCD的面积为24,M、P、N分别是CD、DB、BC上的动点,MP+PN的最小值为2$\sqrt{6}$.
如图,正方形ABCD的面积为24,M、P、N分别是CD、DB、BC上的动点,MP+PN的最小值为2$\sqrt{6}$.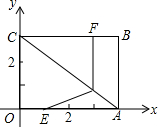 如图在平面直角坐标系中,四边形OABC是矩形,OA=4cm,OC=3cm,动点E、F分别从O、B同时出发,以1cm/s的速度运动,其中,点E眼OA向终点A点运动,点F沿BC向终点C点运动,过点F作FP⊥BC,交AC于点P,连接EP,设运动时间为xs.
如图在平面直角坐标系中,四边形OABC是矩形,OA=4cm,OC=3cm,动点E、F分别从O、B同时出发,以1cm/s的速度运动,其中,点E眼OA向终点A点运动,点F沿BC向终点C点运动,过点F作FP⊥BC,交AC于点P,连接EP,设运动时间为xs.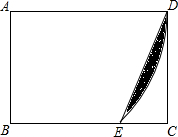 如图,在矩形ABCD中,AB=$\sqrt{2}$,BC=2,以A为圆心,AD为半径画弧交线段BC与E,连接DE,则图中阴影部分的面积为$\frac{π}{2}$-$\sqrt{2}$.(结果保留π)
如图,在矩形ABCD中,AB=$\sqrt{2}$,BC=2,以A为圆心,AD为半径画弧交线段BC与E,连接DE,则图中阴影部分的面积为$\frac{π}{2}$-$\sqrt{2}$.(结果保留π)