题目内容
7.(1)计算:|1-$\sqrt{3}$|-$\sqrt{12}$+2cos30°-20170;(2)解不等式组$\left\{\begin{array}{l}2-x≤3\\ \frac{3}{2}x+1>x-\frac{3}{2}.\end{array}\right.$并求其最小整数解.
分析 (1)首先计算乘方和开方,然后计算乘法,最后从左向右依次计算,求出算式的值是多少即可.
(2)分别求出不等式组中两不等式的解集,找出解集的公共部分确定出不等式组的解集,即可确定出最小的整数解.
解答 解:(1)原式=$\sqrt{3}$-1-2$\sqrt{3}$+$\sqrt{3}$-1
=-2.
(2)$\left\{\begin{array}{l}{2-x≤3①}\\{\frac{3}{2}x+1>x-\frac{3}{2}②}\end{array}\right.$
解不等式①得x≥-1;
解不等式②得x>-5;
不等式组的解集为x≥-1;
最小整数解为-1.
点评 此题考查了实数的运算,以及解一元一次不等式组,熟练掌握运算法则是解本题的关键.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
18.边长为1的正六边形的边心距是( )
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\sqrt{3}$ |
2.下列各式计算正确的是( )
| A. | a+3a2=3a3 | B. | (a-b)2=a2-ab+b2 | C. | 2(a-b)=2a-2b | D. | (2ab)2÷ab=2ab |
19. 如图,AB是⊙O直径,点C为⊙O上一点,∠C=20°,则∠BOC度数为( )
如图,AB是⊙O直径,点C为⊙O上一点,∠C=20°,则∠BOC度数为( )
 如图,AB是⊙O直径,点C为⊙O上一点,∠C=20°,则∠BOC度数为( )
如图,AB是⊙O直径,点C为⊙O上一点,∠C=20°,则∠BOC度数为( )| A. | 20° | B. | 30° | C. | 40° | D. | 60° |
 某学校开展了以“人生观、价值观”为主题的班会活动,活动结束后,九年级某班一小组提出了5个主要观点并在本班50名学生中进行了调查(要求每位同学只选自己最认可的一项观点),并制成了如下扇形统计图.
某学校开展了以“人生观、价值观”为主题的班会活动,活动结束后,九年级某班一小组提出了5个主要观点并在本班50名学生中进行了调查(要求每位同学只选自己最认可的一项观点),并制成了如下扇形统计图.



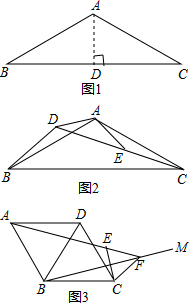 问题背景:如图1,等腰△ABC中,AB=AC,∠BAC=120°,作AD⊥BC于点D,则D为BC的中点,∠BAD=$\frac{1}{2}$∠BAC=60°,于是$\frac{BC}{AB}$=$\frac{2BD}{AB}$=$\sqrt{3}$;
问题背景:如图1,等腰△ABC中,AB=AC,∠BAC=120°,作AD⊥BC于点D,则D为BC的中点,∠BAD=$\frac{1}{2}$∠BAC=60°,于是$\frac{BC}{AB}$=$\frac{2BD}{AB}$=$\sqrt{3}$;