题目内容
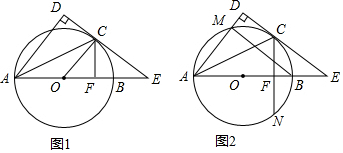
16. 问题背景:如图1,等腰△ABC中,AB=AC,∠BAC=120°,作AD⊥BC于点D,则D为BC的中点,∠BAD=$\frac{1}{2}$∠BAC=60°,于是$\frac{BC}{AB}$=$\frac{2BD}{AB}$=$\sqrt{3}$;
问题背景:如图1,等腰△ABC中,AB=AC,∠BAC=120°,作AD⊥BC于点D,则D为BC的中点,∠BAD=$\frac{1}{2}$∠BAC=60°,于是$\frac{BC}{AB}$=$\frac{2BD}{AB}$=$\sqrt{3}$;迁移应用:如图2,△ABC和△ADE都是等腰三角形,∠BAC=∠DAE=120°,D,E,C三点在同一条直线上,连接BD.
①求证:△ADB≌△AEC;
②请直接写出线段AD,BD,CD之间的等量关系式;
拓展延伸:如图3,在菱形ABCD中,∠ABC=120°,在∠ABC内作射线BM,作点C关于BM的对称点E,连接AE并延长交BM于点F,连接CE,CF.
①证明△CEF是等边三角形;
②若AE=5,CE=2,求BF的长.
分析 迁移应用:①如图②中,只要证明∠DAB=∠CAE,即可根据SAS解决问题;
②结论:CD=$\sqrt{3}$AD+BD.由△DAB≌△EAC,可知BD=CE,在Rt△ADH中,DH=AD•cos30°=$\frac{\sqrt{3}}{2}$AD,由AD=AE,AH⊥DE,推出DH=HE,由CD=DE+EC=2DH+BD=$\sqrt{3}$AD+BD,即可解决问题;
拓展延伸:①如图3中,作BH⊥AE于H,连接BE.由BC=BE=BD=BA,FE=FC,推出A、D、E、C四点共圆,推出∠ADC=∠AEC=120°,推出∠FEC=60°,推出△EFC是等边三角形;
②由AE=5,EC=EF=2,推出AH=HE=2.5,FH=4.5,在Rt△BHF中,由∠BFH=30°,可得$\frac{HF}{BF}$=cos30°,由此即可解决问题.
解答 迁移应用:①证明:如图②
∵∠BAC=∠DAE=120°,
∴∠DAB=∠CAE,
在△DAE和△EAC中,
$\left\{\begin{array}{l}{DA=EA}\\{∠DAB=∠EAC}\\{AB=AC}\end{array}\right.$,
∴△DAB≌△EAC,
②解:结论:CD=$\sqrt{3}$AD+BD.
理由:如图2-1中,作AH⊥CD于H.
∵△DAB≌△EAC,
∴BD=CE,
在Rt△ADH中,DH=AD•cos30°=$\frac{\sqrt{3}}{2}$AD,
∵AD=AE,AH⊥DE,
∴DH=HE,
∵CD=DE+EC=2DH+BD=$\sqrt{3}$AD+BD.
拓展延伸:①证明:如图3中,作BH⊥AE于H,连接BE.
∵四边形ABCD是菱形,∠ABC=120°,
∴△ABD,△BDC是等边三角形,
∴BA=BD=BC,
∵E、C关于BM对称,
∴BC=BE=BD=BA,FE=FC,
∴A、D、E、C四点共圆,
∴∠ADC=∠AEC=120°,
∴∠FEC=60°,
∴△EFC是等边三角形,
②解:∵AE=5,EC=EF=2,
∴AH=HE=2.5,FH=4.5,
在Rt△BHF中,∵∠BFH=30°,
∴$\frac{HF}{BF}$=cos30°,
∴BF=$\frac{4.5}{\frac{\sqrt{3}}{2}}$=3$\sqrt{3}$.
点评 本题考查全等三角形的判定和性质、等腰三角形的性质、四点共圆、等边三角形的判定和性质、锐角三角函数等知识,解题的关键是灵活应用所学知识解决问题,学会添加辅助圆解决问题,属于中考压轴题.

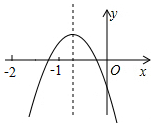 二次函数y=ax2+bx+c(a、b、c是常数,且a≠0)的图象如图所示,下列结论错误的是( )
二次函数y=ax2+bx+c(a、b、c是常数,且a≠0)的图象如图所示,下列结论错误的是( )| A. | 4ac<b2 | B. | abc<0 | C. | b+c>3a | D. | a<b |
 如图所示的几何体,上下部分均为圆柱体,其左视图是( )
如图所示的几何体,上下部分均为圆柱体,其左视图是( )| A. |  | B. |  | C. |  | D. |  |
| A. | a2•a2=2a2 | B. | a2+a2=a4 | C. | (1+2a)2=1+2a+4a2 | D. | (-a+1)(a+1)=1-a2 |
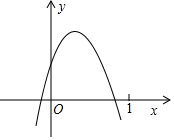 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:①ac>0;②2a+b>0;③y随x的增大而增大;④a-b+c<0,其中正确的个数( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:①ac>0;②2a+b>0;③y随x的增大而增大;④a-b+c<0,其中正确的个数( )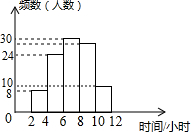 为了解某校学生今年五一期间参加社团活动时间的情况,随机抽查了其中100名学生进行统计,并绘制成如图所示的频数直方图,已知该校共有1000名学生,据此估计,该校五一期间参加社团活动时间在8~10小时之间的学生数大约是( )
为了解某校学生今年五一期间参加社团活动时间的情况,随机抽查了其中100名学生进行统计,并绘制成如图所示的频数直方图,已知该校共有1000名学生,据此估计,该校五一期间参加社团活动时间在8~10小时之间的学生数大约是( )