Question

（1）如图，△ABC是等边三角形，D是BC上一点，点E在BA的延长线上，且BD=AE，证明：CE=DE；
（2）若点D是BC延长线上一点，其余条件不变，上题的结论是否仍然成立？请画出图形，作出判断，并说明理由．

Answer 1

考点：全等三角形的判定与性质

专题：

分析：（1）根据等边三角形的判定与性质，可得∠B=∠F=60°，EF=BE=BF，根据等式的性质，可得BD与CF的关系，根据全等三角形的判定与性质，可得答案；
（2）根据等边三角形的判定与性质，可得∠B=∠F=60°，EF=BE=BF，根据等式的性质，可得BC与DF的关系，根据全等三角形的判定与性质，可得答案．

解答：证明：（1）如图1：延长BC至BF，是BF=BE，连接EF，，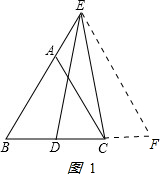
∵△ABC是等边三角形，
∴∠B=60°，AB=BC．
又∵BE=BF，
∴△BEF等边三角形，
∴∠B=∠F=60°，EF=BE=BF．
∵BE-AB=BF-BC，
AE=CF．
∵AE=BD，
∴BD=CF．
在△BDE和△FCE中，

BE=FE ∠B=∠FF BD=FC

，
∴△BDE≌△FCE（SAS），
∴DE=CE；
（2）CE=DE仍然成立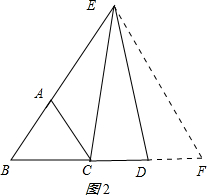，理由如下：
延长BD至BF，是BF=BE，连接EF，
∵△ABC是等边三角形，
∴∠B=60°，AB=BC．
又∵BE=BF，
∴△BEF等边三角形，
∴∠B=∠F=60°，EF=BE=BF．
∵BE-AB=BF-BC，
AE=CF．
∵AE=BD，
∴AB=DF，
BC=DF．
在△BCE和△FDE中，

BE=FE ∠B∠=∠F BC=FD

，
∴△BCE≌△FDE（SAS），
∴DE=CE；

点评：本题考查了全等三角形的判定与性质，利用了等边三角形的判定与性质，全等三角形的判定与性质．