题目内容
已知抛物y=ax2+k经过点A(-1,0)、M(0,1)及x轴上另一点B,直线l∥x轴且与抛物线交于C、D两点,连接AD、BC,若C点横坐标是
,求梯形ABCD的面积.
| 1 |
| 2 |
考点:二次函数的性质,待定系数法求一次函数解析式
专题:计算题
分析:先利用待定系数求出抛物线解析式为y=-x2+1,再根据B点的纵坐标为0,C点的横坐标为
确定它们的坐标,然后根据梯形的面积公式求解.
| 1 |
| 2 |
解答:解:把A(-1,0)、M(0,1)代入y=ax2+k得
,解得
,则抛物线解析式为y=-x2+1;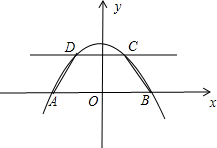
令y=0,则-x2+1=0,解得x=±1,则B点坐标为(1,0);
当x=
时,y=-x2+1=
,则C点坐标为(
,
),
∵直线l∥x轴且与抛物线交于C、D两点,
∴C点和D点是对称点,
而抛物线的对称轴为y轴,
∴D点坐标为(-
,
),
∴梯形ABCD的面积=
×(
+
+1+1)×
=
.
|
|

令y=0,则-x2+1=0,解得x=±1,则B点坐标为(1,0);
当x=
| 1 |
| 2 |
| 3 |
| 4 |
| 1 |
| 2 |
| 3 |
| 4 |
∵直线l∥x轴且与抛物线交于C、D两点,
∴C点和D点是对称点,
而抛物线的对称轴为y轴,
∴D点坐标为(-
| 1 |
| 2 |
| 3 |
| 4 |
∴梯形ABCD的面积=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 4 |
| 9 |
| 8 |
点评:本题考查了二次函数的性质:二次函数y=ax2+bx+c(a≠0)的顶点坐标是(-
,
),对称轴直线x=-
,二次函数y=ax2+bx+c(a≠0)的图象具有如下性质:当a>0时,抛物线y=ax2+bx+c(a≠0)的开口向上,x<-
时,y随x的增大而减小;x>-
时,y随x的增大而增大;x=-
时,y取得最小值
,即顶点是抛物线的最低点;当a<0时,抛物线y=ax2+bx+c(a≠0)的开口向下,x<-
时,y随x的增大而增大;x>-
时,y随x的增大而减小;x=-
时,y取得最大值
,即顶点是抛物线的最高点.
| b |
| 2a |
| 4ac-b2 |
| 4a |
| b |
| 2a |
| b |
| 2a |
| b |
| 2a |
| b |
| 2a |
| 4ac-b2 |
| 4a |
| b |
| 2a |
| b |
| 2a |
| b |
| 2a |
| 4ac-b2 |
| 4a |

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案
相关题目
若xn=2,yn=3,则(xy)3n等于( )
| A、12 | B、16 | C、18 | D、216 |
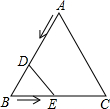 已知△ABC中,AB=AC=BC=6cm.D从A出发以3cm/s速度向B运动,E从B出发以2cm/s的速度向C运动,若D、E同时出发,运动时间为t,问:
已知△ABC中,AB=AC=BC=6cm.D从A出发以3cm/s速度向B运动,E从B出发以2cm/s的速度向C运动,若D、E同时出发,运动时间为t,问:
 (1)如图,△ABC是等边三角形,D是BC上一点,点E在BA的延长线上,且BD=AE,证明:CE=DE;
(1)如图,△ABC是等边三角形,D是BC上一点,点E在BA的延长线上,且BD=AE,证明:CE=DE;