题目内容
已知抛物线y=x2+px+q(q≠0)与x轴交于A(x1,0),B(x2,0)两点,与y轴交于点C,显然,△ABC的形状由系数p、q决定,你能找出关于△ABC的形状和p、q的关系吗?并说明理由.
考点:抛物线与x轴的交点
专题:
分析:当p=0时,则y=x2+q,顶点C在y轴上,A、B关于y轴对称,所以△ABC是等腰三角形,当q2=-q时,由于x1•x2=q,所以q2=OA•OB,即OC2=OA•OB,得出△AOC∽△COB,得出∠ACO=∠CBO,因为∠CBO+∠BCO=90°,所以∠ACO+∠BCO=90°,∠ACB=90°,即可求得△ABC是直角三角形.
解答:解: 当p=0时,△ABC是等腰三角形,当q2=-q时,△ABC是直角三角形;
当p=0时,△ABC是等腰三角形,当q2=-q时,△ABC是直角三角形;
理由:∵当p=0时,则y=x2+q,
∴顶点C在y轴上,
∴AC=BC,
∴△ABC是等腰三角形,
当q2=-q时,
∵x1•x2=q,
∴q2=OA•OB,
即OC2=OA•OB,
∴△AOC∽△COB,
∴∠ACO=∠CBO,
∵∠CBO+∠BCO=90°,
∴∠ACO+∠BCO=90°,
∴∠ACB=90°,
∴△ABC是直角三角形.
 当p=0时,△ABC是等腰三角形,当q2=-q时,△ABC是直角三角形;
当p=0时,△ABC是等腰三角形,当q2=-q时,△ABC是直角三角形;理由:∵当p=0时,则y=x2+q,
∴顶点C在y轴上,
∴AC=BC,
∴△ABC是等腰三角形,
当q2=-q时,
∵x1•x2=q,
∴q2=OA•OB,
即OC2=OA•OB,
∴△AOC∽△COB,
∴∠ACO=∠CBO,
∵∠CBO+∠BCO=90°,
∴∠ACO+∠BCO=90°,
∴∠ACB=90°,
∴△ABC是直角三角形.
点评:本题考查了抛物线和坐标轴的交点与系数的关系,等腰三角形的判定,直角三角形的判定.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
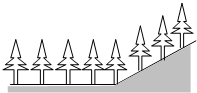 如图,在平地上种植树时,要求株距(相邻两树间的水平距离)为3m.如果在坡度为1:3的山坡上种植树,也要求株距为3m,那么相邻两树
如图,在平地上种植树时,要求株距(相邻两树间的水平距离)为3m.如果在坡度为1:3的山坡上种植树,也要求株距为3m,那么相邻两树间的坡面距离约为( )
| A、4m | B、3m |
| C、5.1m | D、3.2m |
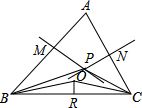 在不等边△ABC中,AB、AC的垂直平分线PM、PN交于点P,∠PBC、∠PCB的角平分线交与Q点,QR⊥BC于点R.求证:P、Q、R三点在同一直线上.
在不等边△ABC中,AB、AC的垂直平分线PM、PN交于点P,∠PBC、∠PCB的角平分线交与Q点,QR⊥BC于点R.求证:P、Q、R三点在同一直线上.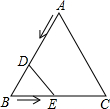 已知△ABC中,AB=AC=BC=6cm.D从A出发以3cm/s速度向B运动,E从B出发以2cm/s的速度向C运动,若D、E同时出发,运动时间为t,问:
已知△ABC中,AB=AC=BC=6cm.D从A出发以3cm/s速度向B运动,E从B出发以2cm/s的速度向C运动,若D、E同时出发,运动时间为t,问:
 (1)如图,△ABC是等边三角形,D是BC上一点,点E在BA的延长线上,且BD=AE,证明:CE=DE;
(1)如图,△ABC是等边三角形,D是BC上一点,点E在BA的延长线上,且BD=AE,证明:CE=DE; 已知O是矩形ABCD的对角线的交点,过点O作OE⊥AC交AB于E,△AOE的面积为5,AE比BC大1,求BD的长.
已知O是矩形ABCD的对角线的交点,过点O作OE⊥AC交AB于E,△AOE的面积为5,AE比BC大1,求BD的长.