题目内容
8.若方程组$\left\{\begin{array}{l}{2x+y=k}\\{2x-y=1}\end{array}\right.$的解中,x是正数,y是非正数.(1)求k的正整数解;
(2)在(1)的条件下求一次函数y=$kx-\frac{3}{2}$与坐标轴围成的面积.
分析 (1)根据方程组得出方程组的解列,再出不等式组解答即可.
(2)把k的值代入得出面积即可.
解答 解:(1)解方程组$\left\{\begin{array}{l}{2x+y=k}\\{2x-y=1}\end{array}\right.$得:$\left\{\begin{array}{l}{x=\frac{k+1}{4}}\\{y=\frac{k-1}{2}}\end{array}\right.$,
因为x是正数,y是非正数,
可得:$\left\{\begin{array}{l}{\frac{k+1}{4}>0}\\{\frac{k-1}{2}≤0}\end{array}\right.$,
解得:-1<k≤1,
因为k取正整数,
所以k=1;
(2)把k=1代入y=$kx-\frac{3}{2}$中,可得y=x-1.5,
所以与坐标轴的面积为$\frac{1}{2}×\frac{3}{2}×\frac{3}{2}=\frac{9}{8}$.
点评 此题考查一次函数的问题,关键是根据方程组得出方程组的解列出不等式组解答.

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
20.表一是甲、乙两名学生这学期的数学测试成绩一览表(单位:分)
表一
已知甲平时成绩的平均分是98分,乙平时成绩的众数是93分,请你完成下列问题:
(1)求表中m和n的值
(2)请求出甲、乙两名学生平时成绩的平均数,中位数、众数和方差,并填写表二
表二
(3)学校规定:学生平时成绩的平均数、期中成绩、期末成绩三项分别按40%、20%、40%的比例计入学期总评成绩,如果总评成绩不少以90分,平时成绩的平均分和期中成绩不变,那么,这两名学生的期末成绩至少应是多少?
表一
| 测试 类别 | 平时成绩 | 期中 | 期末 | ||||
| 测试1 | 测试2 | 测试3 | 测试4 | 测试5 | |||
| 甲 | m | 99 | 100 | 99 | 98 | 96 | 95 |
| 乙 | 90 | 93 | 94 | n | 95 | 92 | 98 |
(1)求表中m和n的值
(2)请求出甲、乙两名学生平时成绩的平均数,中位数、众数和方差,并填写表二
表二
| 学生 | 平均数 | 中位数 | 众数 | 方差 |
| 甲 | 98 | 99 | 99 | 4.4 |
| 乙 | 93 | 93 | 93 | 2.8 |
18.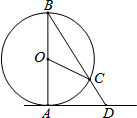 如图,AD是⊙O的切线,A为切点.点C在⊙O上,连接BC并延长交AD于点D,若∠AOC=70°,则∠ADB=( )
如图,AD是⊙O的切线,A为切点.点C在⊙O上,连接BC并延长交AD于点D,若∠AOC=70°,则∠ADB=( )
 如图,AD是⊙O的切线,A为切点.点C在⊙O上,连接BC并延长交AD于点D,若∠AOC=70°,则∠ADB=( )
如图,AD是⊙O的切线,A为切点.点C在⊙O上,连接BC并延长交AD于点D,若∠AOC=70°,则∠ADB=( )| A. | 35° | B. | 45° | C. | 55° | D. | 65° |