题目内容
14.已知(x+y)2=80,(x-y)2=60,求x2+y2及xy的值.分析 根据完全平方公式可知,若将(x+y)2与(x-y)2相加可去除xy项,而二者相减只剩下含xy的项,从而得出结论.
解答 解:(x+y)2+(x-y)2=x2+y2+2xy+x2+y2-2xy=2(x2+y2)=80+60=140,
∴x2+y2=140÷2=70.
(x+y)2-(x-y)2=x2+y2+2xy-x2-y2+2xy=4xy=80-60=20,
∴xy=20÷4=5.
点评 本题考查了完全平方公式的应用,解题的关键是发现“将(x+y)2与(x-y)2相加只剩下x2+y2的倍数,而二者相减只剩下含xy的项”,本题属于简单题型,部分同学解决该类问题时是将完全平方式展开联立,解方程组,这就造成时间上的浪费.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
6.关于函数y=-$\frac{2}{3}$x2的性质描述错误的是( )
| A. | 它的图象关于y轴对称 | |
| B. | 该抛物线开口向下 | |
| C. | 原点是该抛物线上的最高点 | |
| D. | 当x为任意实数时,函数值y总是负数 |
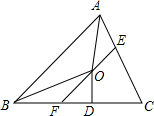 如图,在△ABC中,∠BAC和∠ABC的平分线相交于点O,过点O作EF∥AB交BC于F,交AC于E,过点O作OD⊥BC于D,下列四个结论:
如图,在△ABC中,∠BAC和∠ABC的平分线相交于点O,过点O作EF∥AB交BC于F,交AC于E,过点O作OD⊥BC于D,下列四个结论: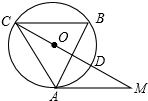 如图,在△ABC中,∠B=60°,⊙O是△ABC的外接圆,过点A作⊙O的切线,交CO的延长线于点M,CM交⊙O于点D.求证:CD=2DM.
如图,在△ABC中,∠B=60°,⊙O是△ABC的外接圆,过点A作⊙O的切线,交CO的延长线于点M,CM交⊙O于点D.求证:CD=2DM.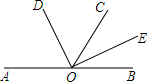 如图,已知A、O、B三点在同一条直线上,OD平分∠AOC,OE平分∠BOC.若∠BOC=62°,求∠DOE的度数.
如图,已知A、O、B三点在同一条直线上,OD平分∠AOC,OE平分∠BOC.若∠BOC=62°,求∠DOE的度数.