题目内容
4.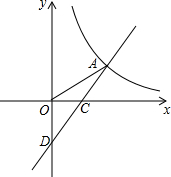 如图,在平面直角坐标系xOy中,一次函数y1=ax+b的图象与反比例函数y2=$\frac{k}{x}$的图象在第一象限内相交于点A(m,2),交x轴、y轴分别于点C、D,且C是AD的中点,S△ODA=4.
如图,在平面直角坐标系xOy中,一次函数y1=ax+b的图象与反比例函数y2=$\frac{k}{x}$的图象在第一象限内相交于点A(m,2),交x轴、y轴分别于点C、D,且C是AD的中点,S△ODA=4.(1)求该反比例函数和一次函数的解析式;
(2)在y轴的右侧直接写出不等式ax+b≤$\frac{k}{x}$的解集.
分析 (1)作AB⊥x轴于B,通过△COD≌△CBA得出OD=AB=2,从而求得D(0,-2),进而根据S△ODA=4求得A的横坐标,然后利用待定系数法即可求得反比例函数和一次函数的解析式;
(2)根据函数的图象即可求得.
解答  解:(1)作AB⊥x轴于B,
解:(1)作AB⊥x轴于B,
在△COD和△CBA中,
$\left\{\begin{array}{l}{∠DCO=∠ACB}\\{∠DOC=∠ABC=90°}\\{DC=AC}\end{array}\right.$
∴△COD≌△CBA(AAS),
∴OD=AB,
∵A(m,2),
∴OD=AB=2,
∴D(0,-2),
∵S△ODA=4.
∴$\frac{1}{2}$OD•xA=4,则xA=4,
∴A(4,2),
把A的坐标代入反比例函数y2=$\frac{k}{x}$得,k=8,
把A、D的坐标代入一次函数y1=ax+b得,$\left\{\begin{array}{l}{2=4a+b}\\{-2=b}\end{array}\right.$
解得$\left\{\begin{array}{l}{a=1}\\{b=-2}\end{array}\right.$,
∴该反比例函数为y2=$\frac{8}{x}$,一次函数的解析式为y1=x-2.
(2)在y轴的右侧,不等式ax+b≤$\frac{k}{x}$的解集为:0<x≤4.
点评 本题考查了反比例函数和一次函数的交点,通过三角形全等和三角形面积求得A、D的坐标是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.以下列长度(单位:厘米)为边的三角形是直角三角形的是( )
| A. | 2,2,3 | B. | 2,3,4 | C. | 3,4,5 | D. | 4,5,6 |
19.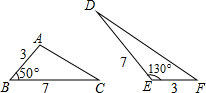 如图,若△ABC和△DEF的面积分别为S1,S2,则( )
如图,若△ABC和△DEF的面积分别为S1,S2,则( )
 如图,若△ABC和△DEF的面积分别为S1,S2,则( )
如图,若△ABC和△DEF的面积分别为S1,S2,则( )| A. | S1=$\frac{1}{2}$S2 | B. | S1=$\frac{7}{2}$S2 | C. | S1=$\frac{8}{5}$S2 | D. | S1=S2 |
16.和温带大陆性气候相比较,温带海洋性气候地区每天气温变化的幅度比较小,较适合人类居住,所以温带海洋性气候地区每天气温的( )比较小.
| A. | 极差 | B. | 平均数 | C. | 众数 | D. | 中位数 |
13. 如图,△ABC的顶点都在正方形网格的格点上,则cosC的值为( )
如图,△ABC的顶点都在正方形网格的格点上,则cosC的值为( )
 如图,△ABC的顶点都在正方形网格的格点上,则cosC的值为( )
如图,△ABC的顶点都在正方形网格的格点上,则cosC的值为( )| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{{\sqrt{5}}}{5}$ | D. | $\frac{{2\sqrt{5}}}{5}$ |
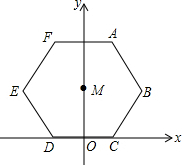 如图,一个边长为2的正六边形ABCDEF的边CD在x轴上,正六边形的中心M在y轴上,现在把这个正六边形沿x轴无滑动的滚动一周,则顶点A的坐标为(13,2$\sqrt{3}$),若滚动100周,中心M经过的路径长400π.
如图,一个边长为2的正六边形ABCDEF的边CD在x轴上,正六边形的中心M在y轴上,现在把这个正六边形沿x轴无滑动的滚动一周,则顶点A的坐标为(13,2$\sqrt{3}$),若滚动100周,中心M经过的路径长400π.
 如图,在△ABC中,点E、F分别为AB、AC的中点.若BC的长为6,则EF的长为3.
如图,在△ABC中,点E、F分别为AB、AC的中点.若BC的长为6,则EF的长为3.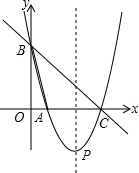 如图,直线y=-x+4与x轴、y轴分别交于点C、B,抛物线y=ax2+bx+c经过点B、C,并与x轴交于另一点A,其顶点为P,tan∠OAB=4.
如图,直线y=-x+4与x轴、y轴分别交于点C、B,抛物线y=ax2+bx+c经过点B、C,并与x轴交于另一点A,其顶点为P,tan∠OAB=4.