Question

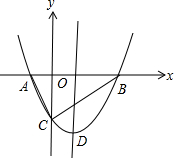如图，抛物线y=

1

2

x²+bx-2与x轴交于A，B两点，与y轴交于C点，且A（-1，0）．
（1）求抛物线的函数关系式及顶点D的坐标；
（2）若点M是抛物线对称轴上的一个动点，求CM+AM的最小值．

Answer 1

考点：抛物线与x轴的交点,轴对称-最短路线问题

专题：

分析：（1）把A的坐标代入抛物线的解析式可求出b的值，进而得到抛物线的解析式，利用配方法即可求出顶点D的坐标；
（2）首先求出C，A，B的坐标，根据抛物线的对称性可知AM=BM．所以AM+CM=BM+CM≥BC=2

5

．

解答：解：（1）∵点A（-1，0）在抛物线y=

1

2

x²+bx-2上，
∴b=-

3

2

，
∴抛物线解析式y=

1

2

x²-

3

2

x-2，
∵抛物线y=

1

2

x²-

3

2

x-2=

1

2

（x-

3

2

）²-

25

8

，
∴顶点D的坐标（

3

2

，-

25

8

）；
（2）当x=0时，y=-2，∴C（0，-2）
∴OC=2，
当y=0时，0=

1

2

x²-

3

2

x-2，
解得：x=4或-1，
∴B（4，0），
∴OB=4，
由抛物线的性质可知：点A和B是对称点，
∴AM=BM，
∴AM+CM=BM+CM≥BC=2

5

．
∴CM+AM的最小值是2

5

．

点评：此题主要考查了待定系数法求二次函数解析式以及抛物线和抛物线的交点问题，利用抛物线的对称性得到AM+CM=BM+CM≥BC=2

5

是解题的关键．