题目内容
8. 如图,点E在y轴上,⊙E与x轴交于点A、B,与y轴交于点C、D,若C(0,9),D(0,-1),则线段AB的长度为( )
如图,点E在y轴上,⊙E与x轴交于点A、B,与y轴交于点C、D,若C(0,9),D(0,-1),则线段AB的长度为( )| A. | 3 | B. | 4 | C. | 6 | D. | 8 |
分析 连接EB,由题意得出OD=1,OC=9,∴CD=10,得出EB=ED=$\frac{1}{2}$CD=5,OE=4,由垂径定理得出AO=BO=$\frac{1}{2}$AB,由勾股定理求出OB,即可得出结果.
解答 解:连接EB,如图所示: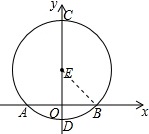
∵C(0,9),D(0,-1),
∴OD=1,OC=9,
∴CD=10,
∴EB=ED=$\frac{1}{2}$CD=5,OE=5-1=4,
∵AB⊥CD,
∴AO=BO=$\frac{1}{2}$AB,OB=$\sqrt{E{B}^{2}-O{E}^{2}}$=$\sqrt{{5}^{2}-{4}^{2}}$=3,
∴AB=2OB=6;
故选:C.
点评 本题考查了垂径定理、坐标与图形性质、勾股定理;熟练掌握垂径定理,由勾股定理求出OB是解决问题的关键.

练习册系列答案
相关题目
16.两个相似三角形的面积比是9:16,则这两个三角形的相似比和周长的比分别为( )
| A. | 9:16;3:4 | B. | 3:4;9:16 | C. | 9:4;9:16 | D. | 3:4;3:4 |
18.将直线y=-2x+1向上平移1个单位,得到一个新的函数是( )
| A. | y=-2x+2 | B. | y=2x+1 | C. | y=-2x-1 | D. | y=-2x |
 二次函数y=ax2+bx+c(a≠0)图象如图,下列结论:
二次函数y=ax2+bx+c(a≠0)图象如图,下列结论: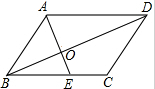 如图,在?ABCD中,E是边BC上的点,分别连结AE、BD相交于点O,若AD=5,$\frac{BO}{DO}$=$\frac{3}{5}$,则EC=2.
如图,在?ABCD中,E是边BC上的点,分别连结AE、BD相交于点O,若AD=5,$\frac{BO}{DO}$=$\frac{3}{5}$,则EC=2. 我国是世界上严重缺水的国家之一.为了增强居民节水意识,某市自来水公司对居民用水采用以户为单位分段计费办法收费.即一月用水10吨以内(包括10吨)的用户,每吨收水费a元;一月用水超过10吨的用户,10吨水仍按每吨a元收费,超过10吨的部分,按每吨b元(b>a)收费.设一户居民月用水x吨,应收水费y元,y与x之间的函数关系如图所示.
我国是世界上严重缺水的国家之一.为了增强居民节水意识,某市自来水公司对居民用水采用以户为单位分段计费办法收费.即一月用水10吨以内(包括10吨)的用户,每吨收水费a元;一月用水超过10吨的用户,10吨水仍按每吨a元收费,超过10吨的部分,按每吨b元(b>a)收费.设一户居民月用水x吨,应收水费y元,y与x之间的函数关系如图所示.