题目内容
19.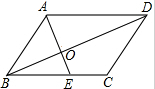 如图,在?ABCD中,E是边BC上的点,分别连结AE、BD相交于点O,若AD=5,$\frac{BO}{DO}$=$\frac{3}{5}$,则EC=2.
如图,在?ABCD中,E是边BC上的点,分别连结AE、BD相交于点O,若AD=5,$\frac{BO}{DO}$=$\frac{3}{5}$,则EC=2.
分析 根据平行四边形的性质得到AD∥BC,AD=BC,推出△BE0∽△DAO,根据相似三角形的性质得到$\frac{BE}{AD}=\frac{BO}{DO}=\frac{3}{5}$,求得BE=3,即可得到结论.
解答 解:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴△BE0∽△DAO,
∴$\frac{BE}{AD}=\frac{BO}{DO}=\frac{3}{5}$,
∵AD=5,
∴BE=3,
∴CE=5-3=2,
故答案为:2.
点评 此题考查了平行四边形的性质以及相似三角形的判定与性质.熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
相关题目
9.三个有理数-2,0,-3的大小关系是( )
| A. | -2>-3>0 | B. | -3>-2>0 | C. | 0>-2>-3 | D. | 0>-3>-2 |




 如图,四边形ABCD中,AB∥CD,AB∥CD,AD∥BC,AC和BD交于点O.
如图,四边形ABCD中,AB∥CD,AB∥CD,AD∥BC,AC和BD交于点O.
 如图,点E在y轴上,⊙E与x轴交于点A、B,与y轴交于点C、D,若C(0,9),D(0,-1),则线段AB的长度为( )
如图,点E在y轴上,⊙E与x轴交于点A、B,与y轴交于点C、D,若C(0,9),D(0,-1),则线段AB的长度为( )