题目内容
3. 如图,已知EG∥AD,∠1=∠G,试说明AD平分∠BAC.
如图,已知EG∥AD,∠1=∠G,试说明AD平分∠BAC.
分析 先根据已知条件推出AD∥EF,再由平行线的性质得出∠1=∠2,∠3=∠G,结合已知通过等量代换即可得到∠2=∠3,根据角平分线的定义可知AD是∠BAC的平分线.
解答 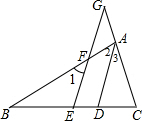 解:∵EG∥AD,
解:∵EG∥AD,
∴∠1=∠2,∠3=∠G,
∵∠G=∠1,
∴∠2=∠3.
∴AD平分∠BAC.
点评 本题考查了平行线的性质和判定,角平分线定义的应用,能正确运用平行线的性质和判定定理进行推理是解此题的关键,注意:平行线的性质是:①两直线平行,同位角相等,②两直线平行,内错角相等,③两直线平行,同旁内角互补,反之亦然.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.教材中“整式的加减”一章的知识结构如图所示,则A和B分别代表的是( )


| A. | 分式,因式分解 | B. | 二次根式,合并同类项 | ||
| C. | 多项式,因式分解 | D. | 多项式,合并同类项 |
8.下列计算错误的是( )
| A. | $\sqrt{2}$×$\sqrt{3}$=$\sqrt{6}$ | B. | $\sqrt{6}$÷$\sqrt{2}$=$\sqrt{3}$ | C. | (-$\sqrt{3}$)2=3 | D. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ |
12. 实数a,b,c,d在数轴上对应点的位置如图所示,这四个数中,倒数最大的是( )
实数a,b,c,d在数轴上对应点的位置如图所示,这四个数中,倒数最大的是( )
 实数a,b,c,d在数轴上对应点的位置如图所示,这四个数中,倒数最大的是( )
实数a,b,c,d在数轴上对应点的位置如图所示,这四个数中,倒数最大的是( )| A. | b | B. | d | C. | a | D. | c |
 如图,∠1的内错角是∠B和∠AEC.
如图,∠1的内错角是∠B和∠AEC.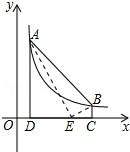 如图,点A(m,6)、B(n,1)在反比例函数图象上,AD⊥x轴于点D,BC⊥x轴于点C,DC=5.
如图,点A(m,6)、B(n,1)在反比例函数图象上,AD⊥x轴于点D,BC⊥x轴于点C,DC=5. 已知:如图,在△ABC中,AB=BC,D是AC中点,点O是AB上一点,⊙O过点B且与AC相切于点E,交BD于点G,交AB于点F.
已知:如图,在△ABC中,AB=BC,D是AC中点,点O是AB上一点,⊙O过点B且与AC相切于点E,交BD于点G,交AB于点F.