题目内容
10．若1＜x＜2，则化简|x-3|-$\sqrt{{x}^{2}-2x+1}$的结果为（ ）| A． | 2x-4 | B． | -2 | C． | 4-2x | D． | 2 |
分析 直接利用x的取值范围，进而化简绝对值和二次根式即可．
解答 解：∵1＜x＜2，
∴|x-3|-$\sqrt{{x}^{2}-2x+1}$
=3-x-（x-1）
=4-2x．
故选：C．
点评 此题主要考查了二次根式的性质与化简以及绝对值的化简，正确把握二次根式的性质是解题关键．
练习册系列答案
金牌课堂练系列答案
三新快车金牌周周练系列答案
相关题目
1．一个盒子中装有四张完全相同的卡片，分别写着2cm，3cm，4cm和5cm，盒子外有两张卡片，分别写着3cm和5cm，现随机从盒中取出一张卡片，与盒子外的两张卡片放在一起，以卡片上的数量分别作为三条线段的长度，那么这三条线段能构成三角形的概率是（ ）
| A． | $\frac{1}{4}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{2}$ | D． | $\frac{3}{4}$ |
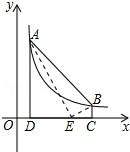如图，点A（m，6）、B（n，1）在反比例函数图象上，AD⊥x轴于点D，BC⊥x轴于点C，DC=5．
已知：如图，在△ABC中，AB=BC，D是AC中点，点O是AB上一点，⊙O过点B且与AC相切于点E，交BD于点G，交AB于点F．
2．
如图，在等腰△ABC中，AB=AC，BD⊥AC，∠ABC=72°，则∠ABD等于（ ）
如图，在等腰△ABC中，AB=AC，BD⊥AC，∠ABC=72°，则∠ABD等于（ ）| A． | 18° | B． | 36° | C． | 54° | D． | 64° |