题目内容
4. 梯形ABCD中,AD∥BC,以A为圆心,DA为半径的圆经过B、C、D三点,若AD=10,BC=16,求梯形ABCD的面积.
梯形ABCD中,AD∥BC,以A为圆心,DA为半径的圆经过B、C、D三点,若AD=10,BC=16,求梯形ABCD的面积.
分析 过A作AM⊥BC于M点,根据垂径定理得到BM=$\frac{1}{2}$BC=8,再在Rt△ABM中,利用勾股定理计算出AM的长,最后利用梯形的面积公式即可得到梯形ABCD的面积.
解答 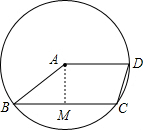 解:过A作AM⊥BC于M点,如图:
解:过A作AM⊥BC于M点,如图:
∴BM=BC,
而AB=AD=10,BC=16,
∴BM=$\frac{1}{2}$BC=8,
在Rt△ABM中,AM=$\sqrt{A{M}^{2}-B{M}^{2}}$=$\sqrt{1{0}^{2}-{8}^{2}}$=6,
∴S梯形ABCD=$\frac{1}{2}$(10+16)×6=78.
点评 本题考查了圆的垂径定理:垂直于弦的直径平分弦,平分弦所对的弧;也考查了勾股定理和梯形的面积公式.

练习册系列答案
相关题目
8.若x=3是方程ax+2x=14-a的解,则a的值为( )
| A. | 10 | B. | 5 | C. | 4 | D. | 2 |
19.已知二次三项式x2-4x+m有一个因式是x+3,求另一个因式以及m的值时,可以设另一个因式为x+n,则x2-4x+m=(x+3)(x+n).
即x2-4x+m=x2+(n+3)x+3n.
∴$\left\{\begin{array}{l}{n+3=-4}\\{m=3n}\end{array}\right.$解得,n=-7,m=-21,
∴另一个因式为x-7,m的值为-21.
类似地,二次三项式2x2+3x-k有一个因式是2x-5,则它的另一个因式以及k的值为( )
即x2-4x+m=x2+(n+3)x+3n.
∴$\left\{\begin{array}{l}{n+3=-4}\\{m=3n}\end{array}\right.$解得,n=-7,m=-21,
∴另一个因式为x-7,m的值为-21.
类似地,二次三项式2x2+3x-k有一个因式是2x-5,则它的另一个因式以及k的值为( )
| A. | x-1,5 | B. | x+4,20 | C. | x$+\frac{3}{2}$,$\frac{15}{2}$ | D. | x+4,-4 |
13. 如图所示,在正方形网格中,图②是由图①经过旋转变换得到的,其旋转中心是点( )
如图所示,在正方形网格中,图②是由图①经过旋转变换得到的,其旋转中心是点( )
 如图所示,在正方形网格中,图②是由图①经过旋转变换得到的,其旋转中心是点( )
如图所示,在正方形网格中,图②是由图①经过旋转变换得到的,其旋转中心是点( )| A. | A点 | B. | B点 | C. | C点 | D. | 无法确定 |
14.下列说法中,正确的是( )
| A. | 两条射线组成的图形叫做角 | B. | 若AB=BC,则点B是AC的中点 | ||
| C. | 两点之间直线最短 | D. | 两点确定一条直线 |
 一个正方体的每个面都有一个汉字,其平面展开图如图所示,那么,在该正方体中与“设”字相对的字是( )
一个正方体的每个面都有一个汉字,其平面展开图如图所示,那么,在该正方体中与“设”字相对的字是( )

