题目内容
20.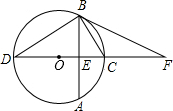 如图,⊙O的直径CD垂直于弦AB,垂足为E,F为DC延长线上一点,且∠CBF=∠CDB.
如图,⊙O的直径CD垂直于弦AB,垂足为E,F为DC延长线上一点,且∠CBF=∠CDB.(1)求证:FB为⊙O的切线;
(2)若AB=8,CE=2,求sin∠BDC.
分析 (1)连接OB,根据圆周角定理证得∠CBD=90°,然后根据等边对等角以及等量代换,证得∠OBF=90°即可证得;
(2)首先利用垂径定理求得BE的长,根据勾股定理求得圆的半径和BC的长,即可得到结果.
解答 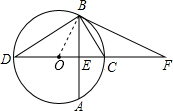 (1)证明:连接OB.
(1)证明:连接OB.
∵CD是直径,
∴∠CBD=90°,
又∵OB=OD,
∴∠OBD=∠D,
又∠CBF=∠D,
∴∠CBF=∠OBD,
∴∠CBF+∠OBC=∠OBD+∠OBC,
∴∠OBF=∠CBD=90°,即OB⊥BF,
∴FB是圆的切线;
(2)解:∵CD是圆的直径,CD⊥AB,
∴BE=$\frac{1}{2}$AB=4,
设圆的半径是R,
在直角△OEB中,根据勾股定理得:R2=(R-2)2+42,
解得:R=5,
在Rt△BEC中,BC=$\sqrt{B{E}^{2}+E{C}^{2}}$=$\sqrt{{4}^{2}+{2}^{2}}$=2$\sqrt{5}$,
在Rt△DBC中,sin∠BDC=$\frac{BC}{CD}$=$\frac{3\sqrt{5}}{10}$=$\frac{\sqrt{5}}{5}$.
点评 本题考查了切线的判定,圆周角定理,勾股定理,三角函数,熟练掌握切线的判定定理是解题的关键.

练习册系列答案
相关题目
5.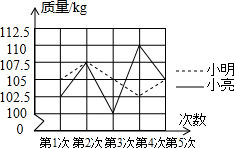 在学校组织的体育训练活动中,小明和小亮参加了举重训练,在近5次的测试中,所测成绩如图所示,请根据图中的信息解答以下问题:
在学校组织的体育训练活动中,小明和小亮参加了举重训练,在近5次的测试中,所测成绩如图所示,请根据图中的信息解答以下问题:
(1)将表格填写完整;
(2)指出小明和小亮哪次成绩最好?
(3)如果从他们两人中挑选1人参加比赛,你认为挑选谁参加比赛更有优势?简单说明理由.
 在学校组织的体育训练活动中,小明和小亮参加了举重训练,在近5次的测试中,所测成绩如图所示,请根据图中的信息解答以下问题:
在学校组织的体育训练活动中,小明和小亮参加了举重训练,在近5次的测试中,所测成绩如图所示,请根据图中的信息解答以下问题:| 第1次 | 第2次 | 第3次 | 第4次 | 第5次 | |
| 小明(kg) | 105 | 107.5 | 105 | 102.5 | 105 |
| 小亮(kg) | 102.5 | 107.5 | 100 | 110 | 105 |
(2)指出小明和小亮哪次成绩最好?
(3)如果从他们两人中挑选1人参加比赛,你认为挑选谁参加比赛更有优势?简单说明理由.
12.下列因式分解变形中,正确的是( )
| A. | 3(x-y)2+2(y-x)=(y-x)(3x-3y+2) | B. | 6(m+n)2-2(m+n)=(2m+n)(3m+n+1) | ||
| C. | -2a2+4a-2=-2(a+1)2 | D. | ab(a-b)-a(b-a)=-a(b-a)(b+1) |
9.数据2,4,3,4,5,3,4的众数是( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
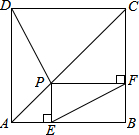 如图,在正方形ABCD中,点P是对角线AC上一点,过点P分别作AB、BC的垂线,垂足为E、F,连接EF.求证:PD=EF.
如图,在正方形ABCD中,点P是对角线AC上一点,过点P分别作AB、BC的垂线,垂足为E、F,连接EF.求证:PD=EF.