题目内容
9.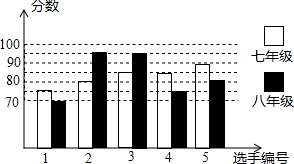 我县某初中举行“中学生与社会”作文大赛,七年级、八年级根据初赛成绩,各选出5名选手组成七年级代表队和八年级代表队参加学校决赛.两个队各选出的5名选手的决赛成绩如图所示.
我县某初中举行“中学生与社会”作文大赛,七年级、八年级根据初赛成绩,各选出5名选手组成七年级代表队和八年级代表队参加学校决赛.两个队各选出的5名选手的决赛成绩如图所示.(1)根据图示填写下表;
| 平均数 (分) | 中位数 (分) | 众数 (分) | |
| 七年级 | 83 | 85 | 85 |
| 八年级 | 83 | 80 | 95 |
(3)计算两队决赛成绩的方差并判断哪一个代表队选手成绩较为稳定.
分析 (1)根据成绩表加以计算可补全统计表.根据平均数、众数、中位数的统计意义回答;
(2)根据平均数和中位数的统计意义分析得出即可;
(3)分别求出初一、初二的方差即可.
解答 解:(1)填表:初二平均数为:$\frac{1}{5}$(75+80+85+85+90)=83(分),
初一众数85(分);初二中位数80(分)
故答案为:83;80;85.
(2)初一成绩好些.因为两个队的平均数都相同,初一的中位数高,
所以在平均数相同的情况下中位数高的初一成绩好些.
(3)∵${S}_{初一}^{2}$=$\frac{1}{5}$[(75-83)2+(80-83)2+(85-85)2+(85-83)2+(90-83)2]=26,
${S}_{初二}^{2}$=$\frac{1}{5}$[(70-83)2+(95-83)2+(95-83)2+(75-83)2+(80-83)2]=106.
因此,初一代表队选手成绩较为稳定.
点评 此题主要考查了平均数、众数、中位数、方差的统计意义.找中位数要把数据按从小到大的顺序排列,位于最中间的一个数或两个数的平均数为中位数;众数是一组数据中出现次数最多的数据,注意众数可以不止一个;平均数是指在一组数据中所有数据之和再除以数据的个数.

练习册系列答案
相关题目
4. 请解答问题:
请解答问题:
(1)某种细胞分裂时由1个分裂成2个,2个分裂成4个,…一个这样的细胞分裂x次后,得到的细胞分裂的个数y与x之间构成一个函数关系,请写出y与x之间的关系可以表示为y=2x;
(2)将此问题一般化,在定义域为全体实数时,试列表研究此函数的图象与性质:
(3)观察图象,请写出你认为正确的结论:①函数的图象是抛物线②函数的图象在一、二象限,y随x的增大而增大③函数图象经过(0,1)点,且与x轴没有交点.
 请解答问题:
请解答问题:(1)某种细胞分裂时由1个分裂成2个,2个分裂成4个,…一个这样的细胞分裂x次后,得到的细胞分裂的个数y与x之间构成一个函数关系,请写出y与x之间的关系可以表示为y=2x;
(2)将此问题一般化,在定义域为全体实数时,试列表研究此函数的图象与性质:
| x | … | -3 | -2 | -1 | 0 | 1 | 2 | 3 | … |
| y |
19.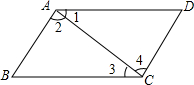 如图,下列判断错误的是( )
如图,下列判断错误的是( )
 如图,下列判断错误的是( )
如图,下列判断错误的是( )| A. | 如果∠2=∠4,那么AB∥CD | B. | 如果∠1=∠3,那么AB∥CD | ||
| C. | 如果∠BAD+∠D=180,那么AB∥CD | D. | 如果∠BAD+∠B=180,那么AD∥CD |
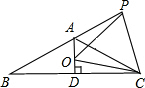 如图,在等腰△ABC中,AB=AC,∠BAC=120°,AD⊥BC于点D,点P是BA延长线上一点,点O是线段AD上一点,OP=OC,若BC=2$\sqrt{3}$,AD=1,则S四边形AOCP=$\sqrt{3}$.
如图,在等腰△ABC中,AB=AC,∠BAC=120°,AD⊥BC于点D,点P是BA延长线上一点,点O是线段AD上一点,OP=OC,若BC=2$\sqrt{3}$,AD=1,则S四边形AOCP=$\sqrt{3}$.