题目内容
17.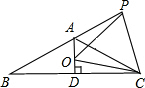 如图,在等腰△ABC中,AB=AC,∠BAC=120°,AD⊥BC于点D,点P是BA延长线上一点,点O是线段AD上一点,OP=OC,若BC=2$\sqrt{3}$,AD=1,则S四边形AOCP=$\sqrt{3}$.
如图,在等腰△ABC中,AB=AC,∠BAC=120°,AD⊥BC于点D,点P是BA延长线上一点,点O是线段AD上一点,OP=OC,若BC=2$\sqrt{3}$,AD=1,则S四边形AOCP=$\sqrt{3}$.
分析 首先在AC上截取AE=PA,易得△APE是等边三角形,继而利用证得△OPA≌△CPE,即可得AC=AO+AP;过点C作CH⊥AB于H,易得S△ABC=$\frac{1}{2}$AB•CH,S四边形AOCP=S△ACP+S△AOC=$\frac{1}{2}$AP•CH+$\frac{1}{2}$OA•CD=$\frac{1}{2}$AP•CH+$\frac{1}{2}$OA•CH=$\frac{1}{2}$CH•(AP+OA)=$\frac{1}{2}$CH•AC,即可得S△ABC=S四边形AOCP.
解答 解:如图1,在AC上截取AE=PA,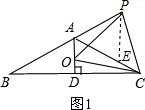 ∵∠PAE=180°-∠BAC=60°,
∵∠PAE=180°-∠BAC=60°,
∴△APE是等边三角形,
∴∠PEA=∠APE=60°,PE=PA,
∴∠APO+∠OPE=60°,
∵∠OPE+∠CPE=∠CPO=60°,
∴∠APO=∠CPE,
∵OP=CP,
在△OPA和△CPE中,
$\left\{\begin{array}{l}{PA=PE}\\{∠APO=∠CPE}\\{OP=CP\\;}\end{array}\right.$,
∴△OPA≌△CPE(SAS),
∴AO=CE,
∴AC=AE+CE=AO+AP;
如图2,过点C作CH⊥AB于H,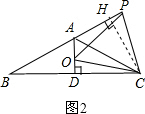 ∵在等腰△ABC中AB=AC,∠BAC=120°,
∵在等腰△ABC中AB=AC,∠BAC=120°,
∴∠DAC=$\frac{1}{2}$∠ABC=60°,∠PAC=180°-∠BAC=60°,
∵∠PAC=∠DAC=60°,AD⊥BC,
∴CH=CD,
∴S△ABC=$\frac{1}{2}$AB•CH,S四边形AOCP=S△ACP+S△AOC=$\frac{1}{2}$AP•CH+$\frac{1}{2}$OA•CD=$\frac{1}{2}$AP•CH+$\frac{1}{2}$OA•CH=$\frac{1}{2}$CH•(AP+OA)=$\frac{1}{2}$CH•AC,
∵AB=AC,
∴S四边形AOCP=S△ABC=$\frac{1}{2}$BC•AD=$\frac{1}{2}$×2$\sqrt{3}$×1=$\sqrt{3}$.
故答案为:$\sqrt{3}$.
点评 此题考查了全等三角形的判定与性质、等边三角形的判定与性质、等腰三角形的性质.注意掌握辅助线的作法,通过证明△OPA≌△CPE得到AC=AO+AP是解题关键,注意数形结合思想的应用.此题综合性很强,难度较大.

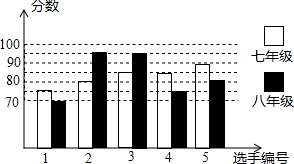 我县某初中举行“中学生与社会”作文大赛,七年级、八年级根据初赛成绩,各选出5名选手组成七年级代表队和八年级代表队参加学校决赛.两个队各选出的5名选手的决赛成绩如图所示.
我县某初中举行“中学生与社会”作文大赛,七年级、八年级根据初赛成绩,各选出5名选手组成七年级代表队和八年级代表队参加学校决赛.两个队各选出的5名选手的决赛成绩如图所示.(1)根据图示填写下表;
| 平均数 (分) | 中位数 (分) | 众数 (分) | |
| 七年级 | 83 | 85 | 85 |
| 八年级 | 83 | 80 | 95 |
(3)计算两队决赛成绩的方差并判断哪一个代表队选手成绩较为稳定.
| A. |  | B. |  | C. |  | D. |  |
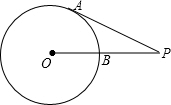 如图,已知PA切⊙O于点A,PO交⊙O于点B,若PA=6,BP=4,则⊙O的半径为2.5.
如图,已知PA切⊙O于点A,PO交⊙O于点B,若PA=6,BP=4,则⊙O的半径为2.5.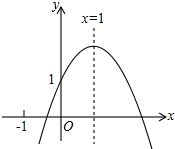 二次函数y=ax2+bx+c(a≠0)的图象如图所示,其对称轴为x=1,有如下结论:①c<1;②2a+b=0;③已知点A(x1,y1),B(x2,y2)在该抛物线上,当x1>x2,则y1>y2;④若方程ax2+bx+c=0有两个根,其中一个根为3,则另一个根为-1,则正确的结论是( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,其对称轴为x=1,有如下结论:①c<1;②2a+b=0;③已知点A(x1,y1),B(x2,y2)在该抛物线上,当x1>x2,则y1>y2;④若方程ax2+bx+c=0有两个根,其中一个根为3,则另一个根为-1,则正确的结论是( )