题目内容
1.北国购物商场销售一批名牌衬衫,平均每天可售出20件,每件盈利40元;为了扩大销售,增加盈利,尽快减少库存,商场决定采取适当的降价措施.经调查发现,每件衬衫每降价1元,商场平均每天可多售出2件.(1)每天销售这种衬衫的盈利要达到1200元,则每件衬衫应降价多少元?
(2)每件衬衫降价多少元时,商场每天盈利最多?利润是多少?
分析 (1)根据:每件的实际利润×降价后的销售量=每天利润,列出方程解方程,再结合题意取舍可得;
(2)根据:每件的实际利润×降价后的销售量=每天利润,列出函数关系式,配方成二次函数顶点式,结合函数性质可得最值情况.
解答 解:(1)设每件衬衫应降价x元,根据题意,
得:(40-x)(20+2x)=1200,
解得:x=10或x=20,
∵商场要尽快减少库存,
∴x=20,
答:每天销售这种衬衫的盈利要达到1200元,则每件衬衫应降价20元;
(2)设每套降价x元,商场平均每天赢利y元,
则y=(40-x)(20+2x)=-2x2+60x+800=-2(x-15)2+1250,
当x=15时,y有最大值为1250元,
答:当每件降价15元时,商场平均每天盈利最多.
点评 本题主要考查二次函数的实际应用能力,准确抓住题目中的相等关系列出方程或函数关系式是解题的关键.

练习册系列答案
相关题目
9.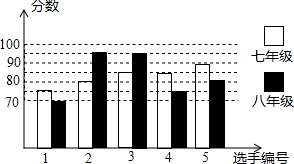 我县某初中举行“中学生与社会”作文大赛,七年级、八年级根据初赛成绩,各选出5名选手组成七年级代表队和八年级代表队参加学校决赛.两个队各选出的5名选手的决赛成绩如图所示.
我县某初中举行“中学生与社会”作文大赛,七年级、八年级根据初赛成绩,各选出5名选手组成七年级代表队和八年级代表队参加学校决赛.两个队各选出的5名选手的决赛成绩如图所示.
(1)根据图示填写下表;
(2)结合两队成绩的平均数和中位数,分析哪个队的决赛成绩较好;
(3)计算两队决赛成绩的方差并判断哪一个代表队选手成绩较为稳定.
 我县某初中举行“中学生与社会”作文大赛,七年级、八年级根据初赛成绩,各选出5名选手组成七年级代表队和八年级代表队参加学校决赛.两个队各选出的5名选手的决赛成绩如图所示.
我县某初中举行“中学生与社会”作文大赛,七年级、八年级根据初赛成绩,各选出5名选手组成七年级代表队和八年级代表队参加学校决赛.两个队各选出的5名选手的决赛成绩如图所示.(1)根据图示填写下表;
| 平均数 (分) | 中位数 (分) | 众数 (分) | |
| 七年级 | 83 | 85 | 85 |
| 八年级 | 83 | 80 | 95 |
(3)计算两队决赛成绩的方差并判断哪一个代表队选手成绩较为稳定.
6.下列图形中既是轴对称图形,又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
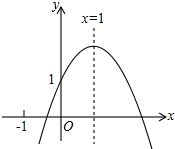 二次函数y=ax2+bx+c(a≠0)的图象如图所示,其对称轴为x=1,有如下结论:①c<1;②2a+b=0;③已知点A(x1,y1),B(x2,y2)在该抛物线上,当x1>x2,则y1>y2;④若方程ax2+bx+c=0有两个根,其中一个根为3,则另一个根为-1,则正确的结论是( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,其对称轴为x=1,有如下结论:①c<1;②2a+b=0;③已知点A(x1,y1),B(x2,y2)在该抛物线上,当x1>x2,则y1>y2;④若方程ax2+bx+c=0有两个根,其中一个根为3,则另一个根为-1,则正确的结论是( )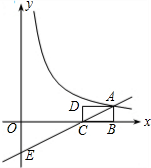 如图,矩形ABCD中,AB=1,BC=2,BC在x轴上,一次函数y=kx-2的图象经过点A、C,并与y轴交于点E,反比例函数y=$\frac{m}{x}$的图象经过点A.
如图,矩形ABCD中,AB=1,BC=2,BC在x轴上,一次函数y=kx-2的图象经过点A、C,并与y轴交于点E,反比例函数y=$\frac{m}{x}$的图象经过点A. 如图,已知,在△ABC中,AB=AC,AD是∠BAC的平分线交BC于点D,E、F分别为AB、AC的中点.求证:四边形AEDF是菱形.
如图,已知,在△ABC中,AB=AC,AD是∠BAC的平分线交BC于点D,E、F分别为AB、AC的中点.求证:四边形AEDF是菱形. 如图,∵∠1=∠2,∴AD∥BC,理由是内错角相等,两直线平行.
如图,∵∠1=∠2,∴AD∥BC,理由是内错角相等,两直线平行.