题目内容
5. 如图,在数轴上A点表示数-3,B点表示数9,若在原点O处放一挡板,一小球甲从点A处以1个单位/秒的速度向左运动;同时另一小球乙从点B处以3个单位/秒的速度也向左运动,在碰到挡板后(忽略球的大小,可看作一点)以原来的速度向相反的方向运动,则经过3或4.2秒,甲球到原点的距离等于乙球到原点的距离的两倍.
如图,在数轴上A点表示数-3,B点表示数9,若在原点O处放一挡板,一小球甲从点A处以1个单位/秒的速度向左运动;同时另一小球乙从点B处以3个单位/秒的速度也向左运动,在碰到挡板后(忽略球的大小,可看作一点)以原来的速度向相反的方向运动,则经过3或4.2秒,甲球到原点的距离等于乙球到原点的距离的两倍.
分析 设经过t秒,甲球到原点的距离等于乙球到原点的距离的两倍.分两种情况:①0<t≤3,②t>3,根据甲球到原点的距离等于乙球到原点的距离的两倍列出关于t的方程,解方程即可.
解答 解:设经过t秒,甲、乙两小球到原点的距离相等.
∵甲球运动的路程为:1•t=t,OA=2,
∴甲球与原点的距离为:t+3;
乙球到原点的距离分两种情况:当0<t≤3时,乙球从点B处开始向左运动,一直到原点O,
∵OB=9,乙球运动的路程为:3•t=3t,乙到原点的距离:9-2t(0≤t≤3);
当t>3时,乙球从原点O处开始一直向右运动,此时乙球到原点的距离为:3t-9 (t>3).
分两种情况:
①当0<t≤3时,得t+3=2(9-2t),解得t=3;
当t>3时,得t+3=2(3t-9),解得t=4.2.
故当t=3或4.2秒时,甲球到原点的距离等于乙球到原点的距离的两倍.
故答案为:3或4.2.
点评 本题考查了一元一次方程的应用,数轴两点间的距离,运用分类讨论思想及数形结合思想是解题的关键.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
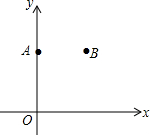 如图,在平面直角坐标系xOy中,点A(0,8),点B(6,8).
如图,在平面直角坐标系xOy中,点A(0,8),点B(6,8). 如图,在△ABC中,AB=AC=10cm,EF是边AB的垂直平分线,且△AEC的周长为24cm,则BC的长=14cm.
如图,在△ABC中,AB=AC=10cm,EF是边AB的垂直平分线,且△AEC的周长为24cm,则BC的长=14cm.