题目内容
15.(2$-\sqrt{5}$)2003•($\sqrt{5}+2$)2004=-2-$\sqrt{5}$.分析 先根据积的乘方得到原式=[(2-$\sqrt{5}$)(2+$\sqrt{5}$)]2003•(2+$\sqrt{5}$),然后根据平方差公式计算.
解答 解:原式=[(2-$\sqrt{5}$)(2+$\sqrt{5}$)]2003•(2+$\sqrt{5}$)
=(4-5)]2003•(2+$\sqrt{5}$)
=-2-$\sqrt{5}$.
故答案为-2-$\sqrt{5}$.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
3.已知等边三角形的高为3,则边长为( )
| A. | 1.5 | B. | 2$\sqrt{3}$ | C. | 6 | D. | $\sqrt{3}$ |
10.若最简二次根式$\sqrt{3a-8}$与$\sqrt{17-2a}$是同类二次根式,则a的取值为( )
| A. | a=4 | B. | a=5 | C. | a=6 | D. | a=7 |
20.下列函数中,属于二次函数的是( )
| A. | $y=\sqrt{{x^2}+1}$ | B. | y=ax2+bx+c | C. | $y=\frac{{{x^2}+1}}{x}$ | D. | $y=-\frac{1}{2}(x+1)(3-x)$ |
4.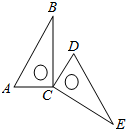 如图一个含30°角的直角三角板ABC绕其直角顶点C旋转到△DCE的位置,当D、E、B三点在同一条直线上时,此时的旋转角∠BCE=( )
如图一个含30°角的直角三角板ABC绕其直角顶点C旋转到△DCE的位置,当D、E、B三点在同一条直线上时,此时的旋转角∠BCE=( )
 如图一个含30°角的直角三角板ABC绕其直角顶点C旋转到△DCE的位置,当D、E、B三点在同一条直线上时,此时的旋转角∠BCE=( )
如图一个含30°角的直角三角板ABC绕其直角顶点C旋转到△DCE的位置,当D、E、B三点在同一条直线上时,此时的旋转角∠BCE=( )| A. | 105° | B. | 120° | C. | 135° | D. | 150° |
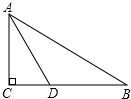 如图所示,在△ABC中,∠C=90°,D点在线段AB的中垂线上,BC=6cm,BD=5cm,那么△ABC的周长是6+2$\sqrt{6}$+2$\sqrt{15}$cm.
如图所示,在△ABC中,∠C=90°,D点在线段AB的中垂线上,BC=6cm,BD=5cm,那么△ABC的周长是6+2$\sqrt{6}$+2$\sqrt{15}$cm. 如图,在数轴上A点表示数-3,B点表示数9,若在原点O处放一挡板,一小球甲从点A处以1个单位/秒的速度向左运动;同时另一小球乙从点B处以3个单位/秒的速度也向左运动,在碰到挡板后(忽略球的大小,可看作一点)以原来的速度向相反的方向运动,则经过3或4.2秒,甲球到原点的距离等于乙球到原点的距离的两倍.
如图,在数轴上A点表示数-3,B点表示数9,若在原点O处放一挡板,一小球甲从点A处以1个单位/秒的速度向左运动;同时另一小球乙从点B处以3个单位/秒的速度也向左运动,在碰到挡板后(忽略球的大小,可看作一点)以原来的速度向相反的方向运动,则经过3或4.2秒,甲球到原点的距离等于乙球到原点的距离的两倍.