题目内容
10．一个圆心角为36°，半径为2的扇形的面积为$\frac{2}{5}$π．分析 根据扇形的面积公式直接代入求得答案即可．
解答 解：S=$\frac{nπ{r}^{2}}{360}$=$\frac{36π×{2}^{2}}{360}$=$\frac{2}{5}$π．
故答案为：$\frac{2}{5}$π．
点评 本题考查了扇形面积公式的应用，掌握圆心角为n°，半径为r的扇形的面积为S=$\frac{nπ{r}^{2}}{360}$．
练习册系列答案
相关题目
20．下列函数中，属于二次函数的是（ ）
| A． | $y=\sqrt{{x^2}+1}$ | B． | y=ax2+bx+c | C． | $y=\frac{{{x^2}+1}}{x}$ | D． | $y=-\frac{1}{2}（x+1）（3-x）$ |
18．使式子$\sqrt{-{x}^{2}}$有意义的x是（ ）
| A． | 全体正数 | B． | 全体负数 | C． | 零 | D． | 非零数 |
如图，在数轴上A点表示数-3，B点表示数9，若在原点O处放一挡板，一小球甲从点A处以1个单位/秒的速度向左运动；同时另一小球乙从点B处以3个单位/秒的速度也向左运动，在碰到挡板后（忽略球的大小，可看作一点）以原来的速度向相反的方向运动，则经过3或4.2秒，甲球到原点的距离等于乙球到原点的距离的两倍．
15．解下列分式方程
（1）$\frac{3}{2x-2}+\frac{1}{1-x}=3$
（2）$\frac{1}{x+3}-\frac{2}{3-x}=\frac{12}{{x}^{2}-9}$．
（1）$\frac{3}{2x-2}+\frac{1}{1-x}=3$
（2）$\frac{1}{x+3}-\frac{2}{3-x}=\frac{12}{{x}^{2}-9}$．
如图，抛物线y=ax2+bx+c交x轴于（-1，0），（2，0），则下列结论：①ac＞0；②a+b=0；③当x$＜\frac{1}{4}$时，y随x的增大而增大；④a-b+c＜0．其中正确的个数有（ ）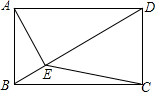
如图，在矩形ABCD中，BC=4，AE⊥BD于E，若∠BAE=30°，则S△ECD=2$\sqrt{3}$．